| |
Computación
Biomolecular: algunos apuntes.
Autores:
Rolando Hong*
Carlos Martínez Ortiz**
Miguel Sautié Castellanos***
Kiria Valdés Crespo****
José Luis Hernández Cáceres*****
Centro de Cibernética Aplicada a la Medicina (CECAM) www.cecam.sld.cu
Índice general
Resumen
Se aborda el problema del desarrollo de sistemas computacionales
basados en la aplicación de principios y soportes procedentes
de la biología.
En opinión de los autores, la investigación en la
frontera de la biología y la física con las tecnologías
de la información puede llevar al desarrollo de nuevos e
importantes sistemas de información (algoritmos y software)
y tecnologías de computación (hardware). La cuestión
es qué y cómo podemos aprender (y entender) de los
sistemas biológicos y físicos y cómo podemos
adoptarlos y adaptarlos para desarrollar las tecnologías
de la información del futuro. La computación biomolecular
y la computación cuántica persiguen estos objetivos.
El hecho de que diferentes tipos de tareas no resueltas hasta el
presente mediante las tecnologías tradicionales encuentre
su soluciónen el marco de la computación biomolecular
puede considerarse como lamejor evidencia de las amplias perspectivas
de este enfoque.
Introducción
El entendimiento de las bases moleculares de la biología molecular
ha crecido enormemente en los últimos años. La célula
puede también ser apreciada como un sistema computacional:
su programa reside en la información genética contenida
en el ADN (ácido desoxiribonucleico), y su estado en la distribución
de los compuestos químicos y cargas eléctricas. El estado
de la célula y el ambiente interactúan con una gran
variedad de expresiones de control y sistemas de transporte para determinar
los estados subsecuentes.
Adleman (Adleman, 1994), fue el primer científico del área
de la computación que logró implementar una tecnología
computacional basada en ideas biológicas. Adleman dio el mejor
de los argumentos para sustentar sus argumentos: llevó a cabo
el cálculo específico usando la tecnología que
describió. En este aspecto, este trabajo es realmente único.
Existen algunas otras tecnologías computacionales basadas en
ideas biológicas que son algo diferentes de las que describió
Adleman; las diferencias en tales sistemas no solo se encuentran en
los sistemas bioquímicos particulares involucrados en el cálculo,
sino también en la naturaleza de los cálculos que cada
sistema puede efectuar.
El sistema propuesto por Adleman descansa en un conocimiento riguroso
de la química, pero no parece dar un propósito de cálculo
general a la maquinaria computacional creada. Algunos intentos de
los sucesores de Adleman para lograr esto no han sido del todo exitosos,
pero de manera general muchos investigadores han aportado rigor matemático
y generalidad al paradigma computacional planteado.
Generalidades en el diseño
de las tecnologías computacionales.
- La representación del estado.
El primer paso que se debe tener en cuenta a la hora de desarrollar
una tecnología computacional es determinar como se debe
representar ‘físicamente’ el estado en que
se encuentra un determinado proceso de computo y esto puede hacerse
de muchas maneras. Un método tradicionalmente usado por
todos los sistemas de computo moderno son las diferencias de potencial
(digamos, por ejemplo en un capacitor).
Los polímeros son moléculas que consisten de unidades
repetidas llamadas monómeros. Algunos polímeros
(incluyendo varias familias importantes de biopolímeros)
son lineales, y por tanto, son cadenas diseñadas a partir
de un alfabeto de monómeros. Por ejemplo, las proteínas,
son polímeros lineales compuestos de veinte aminoácidos
diferentes; las proteínas son, por tanto, cadenas confeccionadas
a partir de un alfabeto de veinte letras.
- Transformación de un estado
El segundo paso en el desarrollo de una tecnología computacional
es mostrar como trasformar un estado; es decir, describir como
la representación física de un estado computacional
puede ser usada para producir la representación física
de un estado sucesivo. En las computadoras mecánicas y
electrónicas, la representación física de
un estado es alterada para producir la representación física
del estado sucesivo: las ruedas dentadas rotan hacia una nueva
posición las cargas eléctricas son transportadas
para crear diferentes diferencias de potencial.
Para llevar a cabo este segundo paso en las computadoras basadas
en polímeros, necesitamos contar con un conjunto suficientemente
grande de transformaciones sobre ellos. Esto conlleva de manera
natural a considerar a los polímeros bioquímicos
y los procesos biológicos, pues las células han
logrado evolucionar una enorme variedad de mecanismos químicos
para manipular biopolímeros.
- Transformaciones iteradas
El paso final, es desarrollar un proceso para iterar las ya mencionadas
transformaciones de estado. Este paso puede ser más difícil
de lo que aparenta a primera vista. Consideremos, por ejemplo,
una computadora electrónica. No es conceptualmente muy
difícil construir un ‘circuito de transformación’
que, dada una representación física de un estado
(en un ‘input’ de registros), use componentes booleanos
estándar que den una determinada respuesta, también
en forma de vector, en registros de salida (o lo que es lo mismo,
un ‘output’ de registros), de tal manera que estos
registros de salida representen el estado sucesivo del calculo
que se está realizando. La parte difícil de este
proceso es tener alguna forma de lograr que estos registros de
salida vuelvan a colocarse en los registros de entrada, de tal
forma que el proceso pueda repetirse una y otra vez. En la práctica,
lograr esto conlleva muchas veces adicionar circuitería
adicional para comunicar la salida con la entrada a expensas de
complicar considerablemente la complejidad general en el diseño
del procesador.
Complejidades algo similares surgen cuando se intenta diseñar
computadoras basadas, por ejemplo, en la traducción del ARN
(ácido ribonucleico).
Propiedades computacionales
estructurales del ADN:
Típicamente los resultados matemáticos han sido usados
para resolver problemas en otras disciplinas científicas,
el trabajo de Adleman se centra en una línea que revierte,
pues se usan técnicas desarrolladas en las ciencias biológicas
en la resolución de un problema matemático (los caminos
hamiltonianos…). Aunque esto no es realmente la primera vez
que ocurre (las ideas biológicas han influenciado otras ramas
del saber), algunos investigadores han propuesto a su vez el nombre
de ‘matemáticas biológicas’ a la nueva
ola de resultados obtenidos en los modelos computacionales surgidos
después del trabajo de Adleman.
A pesar de la complejidad de la tecnología involucrada, la
idea detrás de las ‘matemáticas biológicas’
es realmente la simple observación de que los dos siguientes
procesos (uno biológico y uno matemático) son análogos:
- La estructura compleja de un ser vivo es el resultado de aplicar
operaciones simples (copia, ‘splicing’, etc.) a una
información inicial codificada en una secuencia de ADN.
- El resultado de aplicar una función computable a un argumento
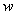 puede obtenerse
aplicando una combinación de funciones básicas simples
a .
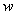Por supuesto que el solo hecho de notar esta similitud no es suficiente.
Adleman, además de notar este hecho, Adleman noto que con
el avance de la biotecnología se podía simular lo
matemático con lo biológico. De manera más
precisa, las cadenas de ADN pueden usarse para codificar información
y las enzimas pueden ser empleadas para simular simples computaciones
y cálculos.
El ADN es una molécula que se encuentra distribuido de manera
muy amplia entre los seres vivos y es normalmente usado como medio
de almacenamiento de la información genética. El ADN
esta compuesto por unidades llamadas nucleótidos que se distinguen
por un grupo químico especifico llamado base nitrogenada.
Las cuatro bases son, adenina, guanina, timina
y citosina, o abreviadamente A, G, T, C. Los nucleótidos
se encuentran enlazados para formar cadenas de ADN. Las secuencias
de ADN tienen una polaridad: una cadena de ADN es distinta de la
cadena revertida. Existe además una complementariedad entre
pares de nucleótidos: A es complementario con T y C es complementario
con G. Las uniones entre sí (en forma lineal) u de manera
complementaria pareada permite la famosa estructura helicoidal de
Watson y Crick. El proceso mediante el cual dos cadenas de ADN complementarias
y de polaridad invertida se unen para formar una doble hélice
se denomina annealing.
El proceso inverso (la separación de la doble hélice
para dar por resultado dos cadenas separadas) se denomina desnaturalización
o melting.
El hecho de que una cadena de ADN se esté formada por una
cadena de cuatro símbolos A, T, C, G, tiene como significado
matemático que podemos contar con un alfabeto de 4 letras
para codificar información, lo cual es más que suficiente,
considerando que las computadoras electrónicas modernas necesitan
solo dos dígitos (0 y 1) para realizar la misma tarea.
Las operaciones simples que pueden llevarse a cabo sobre las secuencias
de ADN en las células pueden realizarse ‘de manera
artificial’ por un número de enzimas que ejecutan tareas
básicas; todas estas enzimas se encuentran disponibles de
manera comercial. Una clase de enzimas llamadas endonucleasas
de restricción, reconocen secuencias cortas especificas
en una determinada cadena de ADN y entonces ‘cortan’
a la cadena en esa posición. Otra enzima, llamada ADN ligasa
se encarga de hacer uniones entre los ‘extremos pegajosos’
de las cadenas de ADN. Existen otras enzimas que podrían
ser potencialmente útiles, pero para los modelos computacionales
planteados por Adleman (y algunos otros investigadores) estas son
suficientes.
El ADN: una estructura de datos
única.
La cantidad de información almacenada por la biología
molecular durante los últimos 40 años es sobrecogedora
por su amplitud. De tal manera y para facilitar la comprensión
de la importancia del ADN en los modelos computacionales planteados,
no se tratarán en demasía los detalles biológicos
y bioquímicos en aras de concentrarnos en la información
que es relevante para la realización de cálculos con
el ADN.
La densidad de datos en el ADN es impresionante. De la misma manera
que una cadena binaria de datos está codificada con ceros
y unos, una cadena de ADN está codificada mediante cuatro
bases, representadas por las letras A, T, C y G.
Las bases (también conocidas como nucleótidos) están
espaciadas cada 0.35 nanómetros a lo largo de la molécula
de ADN, dándole al ADN una gran densidad de datos de aproximadamente
18 Mbits por pulgada. En dos dimensiones si se asume que existe
una base por nanómetro cuadrado, la densidad de datos es
superior a un millón de Gbits por pulgada cuadrada. Compare
esto con la densidad de datos de un disco duro convencional de elevada
eficiencia, el cual tiene aproximadamente 7 Gbits por pulgada cuadrada
(lo cual da un factor de unas 100 000 veces menor).
Otra propiedad importante del ADN es su naturaleza de doble cadena
helicoidal y la propiedad de formar pares de bases complementarias
entre nucleótidos de diferentes cadenas. Esta complementariedad
hace que el ADN sea una estructura de datos única para realizar
cálculos, pues esta propiedad se puede explotar de diferentes
maneras. La corrección de errores es un ejemplo. Los errores
en el ADN ocurren debido a muchos factores. Ocasionalmente, las
enzimas que manipulan el ADN simplemente cometen los errores, haciendo
cortes de la cadena en lugares donde no debían, o insertando
una T por una G. El ADN puede también dañarse por
energía térmica o por la luz ultravioleta proveniente
del sol. Si ocurre un error en una de las cadenas de la doble hélice,
las enzimas de reparación pueden restaurar la secuencia dañada
usando la cadena complementaria como referencia. En algunos sistemas
computacionales se utilizan mecanismos de recuperación de
información análogos a los descritos, sin embargo,
el desarrollo de la tecnología aun no ha permitido usar a
las enzimas de reparación de una manera verdaderamente eficiente
en el almacenamiento y preservación de la información.
Pese a todo, las potencialidades permanecen tentadoras. Es necesario,
sin embargo señalar que la eficiencia en los mecanismos de
reparación naturales del ADN es inferior a los errores de
lectura-escritura de los discos duros actuales.
ADN vs. Silicio
El ADN, con su estructura de datos única y su habilidad para
llevar a cabo muchas operaciones paralelas, permite que se mire
a un problema computacional desde un punto de vista diferente. Las
computadoras basadas en transistores típicamente manejan
las operaciones de una manera secuencial. Por supuesto, también
existen computadoras con muchos procesadores, e incluso los procesadores
modernos incorporan algún procesamiento paralelo, pero en
general, en la arquitectura básica de las computadoras (la
arquitectura de von Neumann), las instrucciones se manejan de manera
secuencial. Una máquina de von Neumann, que es lo que son
todas las computadoras modernas, repite básicamente el mismo
ciclo (‘fetch and execute’) muchas veces. Se direccionan
instrucciones y datos apropiados provenientes de la memoria principal
y luego ejecuta la instrucción, el truco es hacerlo muchas
veces y muy rápido. Las computadoras de ADN, sin embargo,
son máquinas estocásticas que no poseen la arquitectura
de von Neumann y realizan los cálculos de manera diferente
a las computadoras ordinarias con el propósito de resolver
una clase diferente de problemas.
Normalmente, el incremento de la eficiencia en las computadoras
convencionales significa ciclos de reloj más rápidos,
donde el énfasis se encuentra en la velocidad del procesador
y no en el tamaño de la memoria. Por ejemplo, que le dará
a su equipo mayor eficiencia: ¿Duplicar la velocidad del
reloj o duplicar la memoria RAM? En la arquitectura de von Neumann,
duplicar la velocidad del reloj. Para las computadoras de ADN, la
potencia viene de la capacidad de memoria y del procesamiento paralelo.
Si ‘obligamos’ a una computadora de ADN a comportarse
secuencialmente, esta máquina pierde todo su atractivo. Por
ejemplo, observemos la velocidad de lectura y de escritura del ADN.
En las bacterias, el ADN puede replicarse a una velocidad de 500
bases por segundo. Desde el punto de vista biológico esto
es bastante rápido (10 veces más rápido que
las células humanas) y si consideramos las bajas frecuencias
de errores que cometen entonces podemos decir que es un logro impresionante.
Pero esta velocidad es solo unos 1000 bits por segundo, lo cual
es increíblemente lento en comparación con la velocidad
con que los datos pueden salir de un disco duro. Miremos sin embargo
lo que sucede si se permite que muchas copias de las enzimas de
replicación trabajen en paralelo. Antes que todo, las enzimas
de replicación pueden comenzar con la segunda cadena de ADN
incluso antes de que se termine de replicar la primera. De tal manera
que la velocidad de los datos salta a 2000 bits por segundo. Lo
que sucede luego es que el número de cadenas de ADN se incrementa
de manera exponencial (2n después de n iteraciones).
Con cada cadena adicional la velocidad se incrementa en 1000 bits
por segundo, de tal manera que después de 10 iteraciones
el ADN se encuentra replicándose a una velocidad de alrededor
de 1 Mbit por segundo; después de 30 iteraciones, el incremento
es de 1000 Gbits por segundo. Esta velocidad es claramente superior
a las velocidades de datos sostenidas de los mejores discos duros.
Resolución del problema
del camino hamiltoniano (Adleman)
Las posibilidades prácticas de codificar información
en una secuencia de ADN y de llevar a cabo bio-operaciones simples
fue eficientemente usada por Adleman para resolver un ejemplo del
problema del camino Hamiltoniano con un grafo de 7 nodos.
Un grafo G con dos vértices designados Vin y Vout se dice
que tiene un camino Hamiltoniano si y solo si existe una secuencia
de ‘uniones’ entre los nodos e1, e2, e3, e4,... ez,
(es decir, un camino) que comience en Vin y termine en Vout y que
pase por cada vértice exactamente una sola vez.
El siguiente algoritmo (no determinístico) resuelve el problema:
1. Genere caminos aleatorios a través
del grafo.
2. Mantenga durante el cálculo solamente
los caminos que comiencen con Vin o terminen con Vout.
3. Si el grafo tiene n vértices, mantenga
solo los caminos que pasan por exactamente n vértices.
4. Mantenga los caminos que pasan por todos los
vértices del grafo y que pasan por cada uno de ellos solo
una vez.
5. Si al final de la búsqueda queda algún
camino, responda ‘SI’ de otra manera responda ‘NO’.
Para implementar el paso 1, cada vértice
del grafo se codifico como una cadena de ADN aleatoria de una longitud
de 20 nucleótidos. Entonces por cada unión entre vértices
en el grafo, se crea una sea una secuencia de ADN cuya segunda mitad
esta compuesta de la secuencia que codifica el vértice de
origen y la primera mitad de la secuencia codifica para el vértice
de destino. Usando los complementos de los vértices como
molde las secuencias que corresponden a los vértices compatibles
son ‘ligados’ y de esta forma se construyen moléculas
de ADN que codifican caminos aleatorios a través del grafo.
Para implementar el paso 2, el producto del paso
1 se amplifica mediante la reacción en cadena de
la polimerasa (PCR). A partir de este paso solo quedaran los vértices
que comienzan con Vin y terminan en Vout.
Para implementar el paso 3, se usa una técnica
llamada electroforesis en geles, que hace posible la separación
de las cadenas de ADN de acuerdo a su tamaño. Las moléculas
se colocan al inicio de un gel húmedo a través del
cual se aplica un campo eléctrico. Las moléculas de
mayor tamaño se desplazan de manera más lenta en el
gel, después de determinado tiempo las moléculas quedan
separadas en bandas de acuerdo a su tamaño.
El paso 4 se realiza aplicando iterativamente un
proceso llamado purificación por afinidad. Este proceso permite
que solamente las secuencias que contienen una determinada secuencia
correspondiente al vértice v sea filtrada y separada del
resto de las moléculas. Previamente es necesario sintetizar
cadenas complementarias a v y enlazarlas a la matriz de filtrado
del proceso de purificación; solo aquellas cadenas que contienen
la secuencia v quedaran adheridas a las cadenas complementarias
sintetizadas, el resto de las cadenas no será retenida en
la matriz una vez que el flujo de cadenas heterogéneas pasa
a través de la matriz de purificación. Este proceso
se repite con cada resultado de la purificación para cada
uno de los n vértices de nuestro problema inicial.
Para implementar el paso 5 es necesario averiguar
la existencia de una molécula que represente el camino Hamiltoniano.
Esto se hace amplificando los resultados del paso 4 mediante
el PCR y determinando las secuencias de ADN de las secuencias amplificadas
para ver si alguna representa la solución buscada.
Ácido nucleico computacional:
Un modelo de molécula computacional.
Un modelo alternativo al de Adleman fue el propuesto por un equipo
de la universidad de Chicago (Kurtz et al, 1998) es el llamado Ácido
nucleico computacional (CNA). En su aproximación este modelo
plantea que el CNA sea una generalización de ADN, ARN y de
las proteínas, aunque, desde el punto de vista matemático,
es solo una cadena de símbolos sobre un alfabeto finito.
Una molécula de CNA puede replicarse al igual que el ADN.
Una molécula de CNA puede también ser interpretada,
como una molécula de ARNm, para sintetizar una nueva molécula,
en este caso se trataría de sintetizar una nueva molécula
de CNA y no de proteína como ocurre en los sistemas bioquímicos
naturales. Esta molécula sintetizada de CNA puede, a su vez,
ser interpretada para sintetizar una tercera molécula de
CNA y así sucesivamente.
A pesar de que este modelo parece demasiado fantasioso, la molécula
de ARN parece un buen candidato para implementar (o hacer el papel
de) una molécula de CNA. Aunque usualmente pensamos en el
ADN como una doble hélice y el ARN como una molécula
lineal, el ARN también puede formar dobles hélices
en concordancia con las reglas de complementariedad de Watson y
Crick, de tal manera que el ARN puede replicarse mediante un proceso
esencialmente idéntico al proceso de replicación del
ADN. En las células modernas, el ARN no es interpretado por
ribozomas para sintetizar ARN, pero muchos biólogos creen
que las primeras formas de vida estaban basadas puramente el ARN.
En este hipotético ‘mundo de ARN’, las enzimas
estaban construidas a partir de los nucleótidos de ARN más
que de aminoácidos formando estructuras análogas a
los ribozomas. Algunas investigaciones recientes han mostrado además
que el ARN forma enzimas inesperadamente eficientes (ribozimas).
Sobre operaciones lógicas
y aritméticas con el ADN
Es innegable la ventaja del paralelismo masivo de la computación
biomolecular sobre los circuitos electrónicos tradicionales.
Sin embargo, para que la computación con ADN sea aplicable
en un amplio rango de problemas, es necesario que este nuevo modelo
de cálculo pueda soportar operaciones computacionales simples
(Gifford, 1994; Pool, 1995; Rubin, 1996). Los operadores booleanos
tales como AND, OR y NOT, y las operaciones aritméticas tales
como la adición y la sustracción son las operaciones
fundamentales de una computadora electrónica. En contraste
con los problemas de búsqueda que pueden ser resueltos generando
todas las posibles combinaciones y luego extrayendo la respuesta
correcta, para estas operaciones sencillas es necesario que cada
entrada (input) tenga una sola salida o resultado (output). A pesar
de que es poco probable que las tecnologías de computación
biomolecular puedan superar a las técnicas electrónicas
de realizar estos cálculos simples ciertamente (como afirmara
Adleman (1994)) estos nuevos modelos computacionales pueden contribuir
con nuestro entendimiento de la naturaleza de la computación
en sí misma. Se ha realizado algún trabajo simulando
circuitos booleanos y llevando a cabo adiciones y multiplicación
de matrices con ADN. Ogihara y Ray (1997), por ejemplo han mostrado
la manera de simular circuitos booleanos con ADN. Oliver (1996),
ha mostrado como pueden usarse los métodos de cálculo
con el ADN para calcular el producto de matrices booleanas o de
matrices que contienen números reales positivos. Guarnieri
et al (1996) han propuesto una forma muy ingeniosa de adicionar
dos números binarios.
Sobre la universalidad de
las computadoras de ADN.
La computación molecular universal es un tema popular de físicos
(Matzke, 1994) y biólogos (Hammeroff, 1987) y un sueño
de los científicos computacionales (Langton, 1987; Drexler,
1986). Las computadoras moleculares (de llevarse a cabo de manera
eficiente su construcción), no solo serán mucho más
pequeñas que las computadoras tradicionales (almacenaran en
el espacio en que hoy se almacena un bit unos 1012 bits), sino que
también serán más eficientes y rápidas
(lograran unas 1020 operaciones por segundo en comparación
con las 1012 operaciones por segundo de las supercomputadoras actuales
y las 106 operaciones por segundo de las computadoras personales).
En un artículo realmente brillante, Adleman sorprendió
a la comunidad científica al mostrar la posibilidad real de
hacer cálculos con moléculas. Mediante manipulaciones
de ADN logró resolver un problema computacionalmente difícil:
encontrar el circuito Hamiltoniano en un grafo. Luego de esta demostración
espectacular, se han hecho muchas especulaciones acerca de si es posible
que las computadoras moleculares sean capaces de realizar todas las
tareas que las computadoras tradicionales hacen.
Varias investigaciones parecen indicar que la computación molecular
es de hecho universal y puede efectuar todo tipo de cálculo.
Hace ya bastante tiempo, Turing (1936) analizando la naturaleza del
calculo computacional (cuando aun no existían computadoras),
descubrió un modelo teórico de computadoras ‘la
maquina de Turing’ y propuso una tesis de una magnitud impresionante:
‘todo lo que puede ser calculado, puede calcularse en una máquina
de Turing’. Esta tesis es hoy ampliamente aceptada por varias
razones:
- Todo programa sobre toda computadora existente implementa, de
hecho, una máquina de Turing y toda máquina de Turing
puede ser simulada por un programa sobre cualquier computadora
existente.
- Se han descubierto muchos otros modelos computacionales (funciones
recursivas parciales, gramáticas de Chomsky, sistemas de
Post, Calculo lambda de Church, etc.), pero todos ellos han mostrado
ser equivalentes a la máquina de Turing en su poder computacional
(este enunciado se llama ‘tesis de Church’).
Además de los modelos computacionales antes mencionados hace
poco menos de una década se estableció otro modelo computacional
teórico, las ‘multigramáticas de patrones’,
que mostraron también ser equivalentes a la maquina de Turing.
Se ha logrado demostrar que el modelo de computación basado
en procesos biológicos es equivalente a las multigramáticas
de patrones y por tanto a las maquinas de Turing, logrando establecer
de esta manera la universalidad del modelo de computación biológica.
¿Puede el ADN calcular
cualquier cosa?
La ventaja potencial de los cálculos con ADN sobre el cálculo
convencional realizado en computadoras electrónicas está
muy claro para el caso del problema de los caminos Hamiltonianos
y la ruptura de las claves de DES. Por otro lado, estos son solo
problemas particulares resueltos por medio de la biología
molecular. Son experimentos aislados para derivar una solución
combinatoria a un tipo particular de problema. Esto nos lleva
inmediatamente a dos preguntas fundamentales (propuestas ya por
Adleman en su artículo):
1. ¿Qué tipo de problemas
pueden ser resueltos por la computación biomolecular?
2. ¿Será posible, al menos en principio,
diseñar una computadora programable de ADN?
De manera algo más precisa, las preguntas anteriores pueden
ser reformuladas de la siguiente manera:
1. ¿Es el modelo de cálculos
con el ADN computacionalmente completo en el sentido de que la acción
de cualquier función computable (o equivalentemente, el cálculo
sobre cualquier máquina de Turing) puede llevarse a cabo
mediante manipulaciones del ADN?
2. ¿Existe un sistema universal de ADN,
o sea, un sistema que, dada la codificación de una función
computable como dato de entrada, pueda simular la acción
de dicha función para cualquier argumento? (Aquí,
la noción de función corresponde a la noción
de un programa en el cual un argumento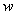
sea la entrada al programa y el valor 
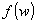sea la salida del programa. La existencia de un sistema universal
de ADN es equivalente, por tanto, a plantear la existencia de una
computadora de ADN capaz de ejecutar programas).
Las opiniones difieren en cuanto a determinar si las respuestas
a estas preguntas tienen alguna relevancia práctica. Podría
discutirse, por ejemplo, que desde el punto de vista practico podría
no ser importante simular una máquina de Turing mediante
un equipo de computación de ADN. De hecho, es probable que
no sea bueno tratar de hacer concordar el modelo de computación
biomolecular con los modelos computacionales clásicos, quizás
sea mejor replantearse nuevamente el problema de los paradigmas
de cálculos computacionales bajo un nuevo modelo. Por otra
parte, encontrar si una clase de algoritmos de ADN es computacionalmente
completa tiene muchas implicaciones prácticas. Si la respuesta
a esta última cuestión fuera desconocida, los esfuerzos
por resolver un problema particular podrían resultar inútiles
en algún momento, pues una persona (quizás influida
por razonamientos Gödelianos) podría de momento anunciar
que tal problema no tiene solución posible mediante manipulaciones
genéticas. El mismo razonamiento es válido para la
prueba teórica de la existencia de una computadora de ADN.
Mientras no se haya encontrado una prueba teórica de que
tal computadora existe, existe gran peligro de que los esfuerzos
prácticos en fabricar tal equipo sean vanos.
Existen otras operaciones y manipulaciones genéticas que
pueden ser usadas para ‘armar’ modelos computacionales
de cálculo. Con todas estas operaciones pueden escribirse
‘programas’ que reciben, por ejemplo, un tubo de ensayo
que contiene cadenas de ADN como datos de entrada y tienen al final
de los cálculos una respuesta de tipo ‘SI’ o
‘NO’, o de lo contrario, pueden producir un conjunto
de tubos de ensayo donde queda codificada la respuesta.
Existen ventajas y desventajas de cada uno de los modelos (combinaciones
de operaciones). Los modelos que usan operaciones similares a las
usadas por Adleman tienen la ventaja que poder ser implementadas
de manera exitosa en el laboratorio. El obstáculo que por
el momento impide la implementación de un proceso de automatización
a gran escala es que la mayor parte de las bio-operaciones dependen
en buena medida de la manipulación manual de los tubos de
ensayo.
En contraste con esto, existe también un modelo introducido
por Tom Head (1987) que pretende ser un modelo ‘de un solo
compartimento’, con un solo tubo de ensayo en el que se realicen
todas las operaciones mediante vías enzimáticas, a
esta nueva familia de sistemas introducidas por Head se le conoce
de manera general como sistemas de splicing. El modelo
de Head tiene, además, la ventaja de ser un modelo matemático,
donde todos los hallazgos están basados en rigurosas pruebas
matemáticas. Su desventaja es que el estado actual de la
biología molecular no permite aun implementaciones prácticas
de este sistema. De manera general, la existencia de diferentes
modelos con características muchas veces complementarias
muestra la versatilidad de los cálculos con ADN e incremente
la probabilidad de que algún día se fabriquen equipos
funcionales basados en esta tecnología.
Sobre las tareas y problemas que debe
enfrentar la computación biomolecular.
La computación biomolecular es un terreno nuevo, con metodologías
aun bastante inexploradas. Es un terreno por naturaleza interdisciplinario,
teniendo muchas interfaces entre la biología y las ciencias
de la computación.
Objetivos y principales aplicaciones de la computación
biomolecular.
- Búsqueda de problemas NP-completos. Los problemas NP-completos
son una clase de problemas computacionales que requieren una gran
búsqueda combinatoria para alcanzar la solución,
pero que requieren un trabajo relativamente modesto para verificar
si la solución dada es correcta. Los problemas de búsqueda
en la solución de problemas NP-completos se resuelven en
la computación biomolecular mediante el ensamblaje de un
gran número de soluciones potenciales, donde cada solución
potencial se encuentra codificada en una molécula de ADN;
luego se llevan a cabo operaciones de la tecnología de
ADN recombinante para separar las soluciones correctas del problema.
(Ejemplo: Adleman y su solución del ‘traveling salesman
problem’).
- Incrementar la capacidad de memoria. La computación biomolecular
tiene el potencial de poder implementar enormes cantidades de
memoria. Un pequeño volumen puede contener un gran número
de moléculas. Una solución acuosa de ADN (con algunas
sales y otros compuestos) puede contener aproximadamente de 107
a 108 tera-bytes, y pueden realizarse búsquedas paralelas
masivas sobre este volumen de información.
- Procesamiento paralelo. Como ya hemos visto, la computación
biomolecular también tiene el potencial de implementar
aplicaciones masivamente paralelas. En este caso puede pensarse
en cálculos en los que cada estado del procesador este
representado por una hebra de ADN. Desde este punto de vista,
puede pensarse en almacenar en un litro de solución de
ADN unos 1018 procesadores.
- Nano-fabricación y autoensamblaje de ADN. Las técnicas
de la computación biomolecular combinadas con las técnicas
de nano-fabricación de ADN pueden permitir el autoensamblaje
de ADN en enrejados bi y tridimensionales; estas estructuras espaciales
pueden usarse para codificar cálculos en formas mucho más
complejas.
Sobre la complejidad
de los problemas que debe resolver la computación biomolecular.
Un hecho importante acerca del resultado de Adleman es que no solo
da una solución a un problema matemático dado, sino
que además, el problema que resuelve es computacionalmente
difícil de resolver.
Los problemas pueden ser ordenados de acuerdo al tiempo que le toma
al mejor algoritmo resolverlos cuando se ejecutan sobre una sola
computadora. Los algoritmos cuyo tiempo de corrida están
‘limitados’ o regidos por una función polinómica
dada en términos del tamaño de los datos de entrada
que describen el problema están en la clase P ‘de tiempo
polinómico’. Respectivamente si la función es
exponencial los problemas caen en la clase EXP ‘de tiempo
exponencial’. Un problema se dice que intratable
si es computacionalmente tan difícil que ningún algoritmo
de tiempo polinómico puede resolverlo.
Una clase especial de problemas, aparentemente intratables,
que incluyen a P e incluidos en EXP es la clase NP ‘no-determinísticos
de tiempo polinómico’. La siguiente relación
entre clases de problemas se cumple:
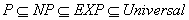
NP contiene los problemas para los cuales no se conoce un algoritmo
que los pueda resolver en un tiempo polinómico, pero que
pueden ser resueltos en tiempo polinómico usando una computadora
no-determinística (esto es, una computadora que tenga la
habilidad de llevar a cabo un número ‘ilimitado’
de búsquedas paralelas de manera independiente). El problema
de los caminos Hamiltonianos es un tipo especial de problema NP
conocido como ‘NP-completo’. Un problema NP-completo
tiene la propiedad de que todo problema en NP puede ser reducido
a él en tiempo polinómico. Por tanto, en determinado
sentido, los problemas NP-completos son los problemas más
difíciles en NP.
La pregunta de si los problemas NP-completos son intratables (o
matemáticamente formulado ¿Es P igual a NP?) se considera
como uno de los problemas más importantes en las matemáticas
y las ciencias computacionales modernas.
Debido a que se sabe que el problema de los caminos hamiltonianos
es un problema NP-completo, parece muy probable que no exista un
algoritmo eficiente (esto es, en tiempo polinómico) para
resolverlo con una computadora electrónica.
Sobre los errores
Adleman, sin embargo, señala que a medida que el tamaño
del problema computacional combinatorio (como el tratado por él
en su articulo) crece debe prestarse especial atención, pues
aumenta la probabilidad de formación de ‘pseudocaminos’,
es decir, falsos positivos. Precisamente en el paso de purificación
por afinidad deben reducirse enormemente la cantidad de falsos positivos
que se pudieran presentar. Este paso, sin embargo, es el paso más
lento, y debe ser eliminado o modificado para hacer que el método
tenga alguna implementación practica eficiente.
Para hacer de los cálculos basados en ADN una técnica
confiable, el primer paso es asegurarse de que no ocurran errores.
Si ocurren muchas hibridaciones incorrectas, entonces los falsos positivos
(cadenas de ADN que parecen ser soluciones validas pero no lo son)
y los falsos negativos pueden surgir durante el cálculo. La
probabilidad de que ocurra una hibridación imperfecta depende
de las condiciones de reacción, tales como las concentraciones
de sodio, pH, temperatura, por ciento relativo de (A+T)’s y
(C+G)’s y longitud del ADN. De estos factores, la temperatura
es él más importante.
Una muestra de poder: el ataque a
DES.
Una aplicación interesante que se desarrollo en computaciones
moleculares con problemas complejos fue el planteamiento de un ‘programa
molecular’ especialmente diseñado para quebrar el Estándar
de Encriptación de Datos (DES) del gobierno de los Estados
Unidos (Boneh et al, 1995). DES encripta un mensaje de 64 bits y
usa una llave de 56 bits. Hacer quebrar DES significa que dado un
par texto-normal, texto-cifrado, se pueda encontrar una llave que
realice el ‘mapeo’ entre los dos textos presentados
al algoritmo. Un ataque convencional a DES normalmente necesita
llevar a cabo una búsqueda exhaustiva sobre las 256
posibles llaves de DES, lo cual, a una velocidad de 100 000 operaciones
por segundo tomaría unos 10 000 años. En contraste,
se ha estimado que DES puede ser quebrado usando computaciones moleculares
en 4 meses de trabajo de laboratorio. Luego del éxito de
Adleman en la implementación practica de la solución
al problema de los caminos Hamiltonianos y con este calculo acerca
de las potencialidades de la tecnología de computación
biomolecular muchos otros investigadores han migrado a este nuevo
campo de trabajo no solo por el interés intelectual que representa,
sino también gracias a una buena cantidad de dinero que se
ha dedicado a la investigación en el área. En particular
la ‘National Science Foundation’ de los estados Unidos
y la ‘Defense Advanced Research Project Agency’ del
Pentágono tienen un gran interés en invertir en estos
temas. La mayor parte de las motivaciones de los militares surge
a partir del incremento de la calidad de las técnicas de
encriptación que otros países usan para codificar
sus datos. Como resultado, Washington necesitará computadoras
cada vez más poderosas para romper los códigos de
otros países.
El problema mencionado anteriormente muestra claramente que la computación
molecular tiene el potencial de superar la eficiencia de las computadoras
existentes hoy día. Una de las razones es que las operaciones
que se usan actualmente en biología molecular pueden ser
organizadas para realizar búsquedas paralelas masivas.
Catenanos: un avance tecnológico
hacia la construcción eficiente de computadoras moleculares.
Recientemente un grupo de investigación de la Universidad
de California Los Angeles (UCLA) reportaron en la revista Science
que habían construido un interruptor molecular (‘switch’)
que podía ser apagado y encendido miles de veces (tomado
de News in Science, 2000). Este mismo grupo ya había reportado
la construcción de otro interruptor molecular que solo podía
ser apagado o encendido una sola vez.
Este avance tecnológico nos acerca la posibilidad de construir
computadoras moleculares muy eficientes basadas en el uso de compuertas
lógicas. El interruptor molecular permitiría la realización
de operaciones binarias usado de manera tan extensiva en las computadoras
digitales comunes. Existe, por supuesto un gran interés en
esta área debido a que las computadoras moleculares podrían
potencialmente ser mucho más baratas que las actuales, sin
contar con las facilidades de miniaturizacion que podrían
aportar.
La investigación del equipo de la UCLA se basa en la síntesis
de unas moléculas llamadas ‘catenanes’ (¿catenanos?),
que están compuestas por dos anillos de átomos interconectados.
El interruptor funcional se establece bajo la posibilidad que tienen
estos dos anillos de pasarse un electrón de uno a otro anillo.
Estas moléculas tienen la habilidad de reconocerse una a
otra y alinearse de una manera eficiente. Previamente se usaron
moléculas de roxetanos, pero estas moléculas debían
estar en solución y su disposición espacial era, por
tanto, mucho más desorganizada.
El desarrollo de una memoria RAM (Random Access Memory) molecular
siempre ha sido una de las principales barreras de la computacion
molecular, pero esta investigación también trae esta
posible aplicación a un paso más cercano de la realidad.
La combinación de esta tecnología de miniaturización
con las tecnologías digitales ya ampliamente usadas y el
uso conjunto de otros modelos computacionales (computador cuántico,
computador de ADN) promete un futuro muy interesante para las tecnologías
computacionales.
Computadoras de ADN autopropulsadas
Un equipo de investigaciones liderado por el estudiante doctoral
Yaakov Benenson del Instituto Weizmann de Ciencias ha descubierto
que una sola molécula de ADN puede brindar toda la energía
necesaria para realizar un calculo computacional (Tomado de News
in Science, 2003). Este es realmente el primer bosquejo de una especie
de computadora muy pequeña. El reporte de esta investigación
se realizo en la revista Proceedings of The National Academy of
Science.
La máquina es tan pequeña que una pequeña gota
podría contener hasta 3 trillones de estas computadoras de
ADN, y pueden efectuar unos 66 billones de operaciones por segundo.
Este mismo laboratorio del Instituto Weizmann hizo ya un aporte
significativo en el 2001 cuando su líder, el profesor Enud
Shapiro patento un diseño de computadoras de ADN que fue
noticia ese año en los titulares de varias revistas especializadas
y prensa de divulgación científica. El hallazgo de
Shapiro fue en verdad la primera computadora autónoma programable
en la cual todo (input, output, software, hardware) estaba hecho
de ADN. Esta computadora podía llevar a cabo un billón
de operaciones por segundo con una eficacia del 99.8%.
El nuevo diseño de Benenson, incorpora un proceso bioquímico
que genera suficiente cantidad de energía (calor) como para
hacer que el equipo sea autónomo, esto significa que, en
principio, las computadoras de ADN pueden funcionar sin una fuente
externa de energía.
Las computadoras electrónicas convencionales procesan información
(en forma de pulsos eléctricos) a través de circuitos
pagados a chips de silicio, pero la tecnología ya se esta
acercando a los limites teóricos de miniaturización.
Los tecnólogos esperan que en algún momento entre
el 2010 y el 2015, la larga marcha de la ley de Moore (que plantea
que el poder computacional se duplique cada 18 meses aproximadamente)
se detenga bruscamente.
Los cómputos bioquímicos ofrecen la promesa de un
mayor poder de procesamiento de información y capacidad de
almacenamiento en un menor espacio, adaptando usados en la naturaleza
por las ‘máquinas biomoleculares’ que se encuentran
en las células vivas. Se ha estimado que un gramo de ADN
seco contiene tanta información como un trillón de
discos compactos.
Las computadoras de ADN representan la información como patrones
de moléculas ordenadas a lo lardo de una cadena de ADN, y
usan enzimas para llevar a cabo reacciones químicas que cambian
de manera predecible estos patrones o los copian. Se han propuesto
muchos diseños, pero todos recaen en el uso de la molécula
de ATP como fuente de energía.
La nueva computadora usa enzimas naturales como hardware. Cada paso
computacional requiere dos moléculas complementarias de ADN,
una que actúa como ‘input’ y otra que actúa
como software. Estas moléculas se unen espontáneamente
y entonces la molécula que funciona como software le indica
a una enzima que corte un determinado segmento de la molécula
que actúa como dato de entrada o input. La ruptura del enlace
en la cadena de ADN libera la energía necesaria que se encuentra
almacenada precisamente en el enlace que se acaba de romper.
El naciente campo de la computación con ADN esta basado en
la comprensión cada vez mayor de la maquinaria molecular
de la vida, y ofrece una visión nueva y refrescante de cómo
los sistemas vivos han evolucionado para crear un equipo muy eficiente
de procesamiento de información –la célula-.
A pesar de que el potencial de las computadoras de ADN ha sido cuestionado
por algunos científicos, Shapiro ha dicho que él cree
que eventualmente será posible colocar las computadoras de
ADN dentro del cuerpo humano para identificar e incluso corregir
fallos en el funcionamiento liberando las drogas apropiadas.
Comentarios finales
Las computadoras actuales de silicio están comenzando a mostrar
sus limitaciones: se están alcanzando los límites
impuestos por las leyes de la física en cuanto a la miniaturización
de los componentes necesaria para
aumentar la velocidad de proceso y la capacidad de almacenamiento
en las memorias de silicio está siendo sobrepasada con creces
por otras tecnologías (memorias holográficas, ADN).
La barrera de los pentaflops (1015 operaciones por segundo) necesaria
para complejos problemas de simulación y optimización
y para muchos problemas de la IA no se alcanzará con computadoras
paralelas de silicio clásicas.
La computación biomolecular (con ADN, ARN, proteínas,
o con membranas) o la computación cuántica quizás
no sustituyan a los semiconductores de silicio en los PC's que tenemos
sobre nuestras mesas pero probablemente entren en juego como potentes
tecnologías de la futura super-computación paralela
avanzada. Estos nuevos modelos no convencionales no son simples
mejoras sobre modelos anteriores de cómputo sino que aprovechan
el paralelismo inherente de los procesos biológicos (ensamblaje
o hibridación del ADN) y de los procesos físicos (superposición
de estados cuánticos).
La frontera entre los problemas `tratables' y los `intratables'
o no resolubles de forma eficiente ha permanecido prácticamente
inalterada durante los últimos 40 años. La computación
cuántica ha desplazado esta frontera y ha mostrado su hegemonía
(al menos teórica) frente a los modelos de cómputo
clásicos (máquinas de Turing, RAM, circuitos) al comprobarse
que pueden resolver en tiempo polinómico problemas que cualquier
modelo clásico resolvería en tiempo exponencial; por
ejemplo, el problema de la factorización de números,
de gran importancia en la criptografía actual.
Creemos que la investigación en la frontera de la biología
y la física con las tecnologías de la información
puede llevar al desarrollo de nuevos e importantes sistemas de información
(algoritmos y software) y tecnologías de computación
(hardware). La cuestión es qué y cómo podemos
aprender (y entender) de los sistemas biológicos y físicos
y cómo podemos adoptarlos y adaptarlos para desarrollar las
tecnologías de la información del futuro. La computación
biomolecular y la computación cuántica persiguen estos
objetivos.
El avance tecnológico actual está permitiendo manipular
de forma cada vez más precisa la materia a nivel molecular
e incluso atómico. Estos avances tecnológicos pueden
hacer realidad estos dos nuevos modelos de computación. En
el siglo XX se han intentado simular procesos computacionales presentes
en la Naturaleza. En el siglo XXI, los esfuerzos se encaminarán
a utilizar la propia Naturaleza para realiza cómputos. Estos
estudios nos permitirán también descifrar las leyes
del procesamiento de la información en la Naturaleza. Una
teoría única de la información que incluya
la física, la computación y la biología.
Bibliografia
Adleman L. Molecular computation of solutions to combinatorial
problems. Science, 266: 1021-1024, 1994.
Kurtz S.A., Mahaney S.R., Royer J.S., Simon J. Biological Computing.
In Complexity Theory Retrospective II. Edited by L.A. Hemaspaandra,
A.L. Selman. Springer Verlag, 1998.
Drexler K.E. Engines of creation: the coming era of nanotechnology.
Anchor Press, 1986.
Hammerroff S.R. Ultimate computing: Biomolecular consciousness and
nanotechnology. N. Holland, 1987.
Matzke D. Proc. Workshop on Physics and computation. PhysCom’94.
IEEEComp.Sci.Press 1994 ISBN 0-8186 6715-X.
Turing A.M. On computable numbers, with an application to the Entschcidungsproblem.
Proceedings of the London Mathematical Society, 42: 230-265, 1936.
Boneh D., Dunworth C., and Lipton R. Breaking DES using a molecular
computer. In Proceedings of DIMACS workshop on DNA computing, 1995.
published by the AMS.
Head T. Formal language Theory and DNA: an analysis of the generative
capacity of recombinant behaviours. Bulletin of Mathematical Biology,
49: 737-759, 1987.
Gifford D.K. On the path to computation with DNA. Science, 266:
993-994, November 1994.
Pool R., A boom in plans for DNA computing. Science, 268:498-499,
April 1995.
Rubin H., Looking for the DNA killing app. Natural Structural Biology,
3(8):656-658, August 1996.
Ogihara M., Ray A., Simulating boolean circuits on a DNA computer.
In 1rst Annual Conference on Computational Molecular Biology, pages
326-331, 1997.
Oliver J.S., Computation with DNA-matrix multiplication. In 2nd
Annual Meeting on DNA based computers, June 1996.
Guarnieri F., Fliss M., Bancroft C., Making DNA add. Science, 273
(5272): 220-223, July 1996.
News in Science. August 28, 2000. http://www.abc.net.au/science/news/stories/s168118.htm
News in Science. February 25, 2003. (Bob Beale)
http://www.abc.net.au/science/news/stories/s792007.htm
|
