Apuntes sobre Representación Gráfica.
<Resumen> <Introducción><Objetivo><Conclusiones> <Bibliografía>
<Desarrollo>
- Gráfico de barras simples.
- Gráfico circular, de sectores o pastel.
- Gráfico de barras múltiples.
- Gráfico de barras compuestas.
- Histograma.
- Polígono de frecuencias.
- Gráfico de frecuencias acumuladas u ojiva.
- Gráfico aritmético simple.
Autores: Lic. René Arenas Gutiérrez
Lic. Juana María Romero del Sol
Lic . Katia García Hernández
Lic. Guillermo Pérez Llánez
Lic. Luisa Pacios Fernández
Facultad de Ciencias Médicas “Julio Trigo López”
RESUMENLos resultados de los estudios deben presentarse en forma clara y correcta a fin de que puedan utilizarse adecuadamente. Este trabajo da algunas definiciones y explica procedimientos para la presentación gráfica de la información (gráficos más comunes) de acuerdo a lineamientos reconocidos internacionalmente, ya que con frecuencia se cometen errores y los gráficos están mal confeccionados. Permite al lector mejorar la presentación del contenido científico. Se ponen ejemplos de gráficos elaborados de forma sencilla en las aplicaciones de Microsoft Office, como usualmente lo hacen las personas no expertas.
Palabras clave: gráfico, barras, frecuencias, variable
En muchas ocasiones la información proporcionada en una tabla es tan singular o importante que se decide presentar esos resultados de forma gráfica. Cuando se decide utilizar el gráfico, este sustituye a la tabla, no la complementa. Por ello no se deben tener tantos gráficos como tablas. Como se presenta sólo uno de los dos, se acostumbra reflejar la información numérica en el gráfico para que no sea necesaria la tabla correspondiente. Incluso, un número innecesariamente grande de gráficos le puede restar lucidez al trabajo en lugar de proporcionarle calidad o rigor científico. Se debe lograr un balance entre estas dos formas de presentación de resultados (1).
El objetivo básico de un gráfico es transmitir la información de forma tal que pueda ser captada rápidamente, de un golpe de vista. Luego, un gráfico debe ser ante todo sencillo y claro, a pesar de su aspecto artístico, ya que se elabora para ser incluido en un trabajo científico.
Existen múltiples tipos de gráficos, pero aquí trataremos solamente de los usados más frecuentemente, que son: gráfico de barras simples, gráfico de sectores o circular (pastel), gráfico de barras múltiples, gráfico de barras compuestas, histograma, polígono de frecuencias, gráfico de frecuencias acumuladas y gráfico aritmético simple. También haremos una breve referencia a otros tipos de gráfico utilizados en ciertos temas del campo de la Medicina, como son los gráficos semilogarítmicos, los probabilísticos y los logísticos (2).
Explicar los elementos básicos necesarios a tener en cuenta para realizar una correcta representación gráfica de los datos.
Veamos primeramente algunos principios comunes en la construcción de gráficos:
· En su gran mayoría los gráficos se inscriben en un sistema de ejes coordenados, siendo el circular o de sectores una excepción.
· En uno de los ejes se representan las frecuencias observadas o los valores calculados a partir de los datos, mientras que en el otro se representa el criterio principal de clasificación (que aparece en el talón de la tabla correspondiente).
· La escala relativa al eje donde se representan frecuencias debe comenzar en cero. De ser necesario, se puede interrumpir 'adecuadamente' la escala. Decimos adecuadamente porque la forma de realizar esa ruptura depende del tipo de gráfico.
· La longitud de un eje debe ser, aproximadamente, entre una vez y una vez y media la del otro. Esta proporcionalidad es importante, pues garantiza la comparabilidad entre gráficos.
· Cada eje debe ser rotulado, es decir, indicar que representa, y en caso de que corresponda, la unidad de medida usada.
· Un gráfico no debe sobrecargarse de líneas o cifras, el solo da la idea general del fenómeno, pues los detalles están representados en la tabla correspondiente (3).2.- Componentes de un gráfico.
Un gráfico, al igual que una tabla, está compuesto de las partes siguientes:a.- Identificación del gráfico.
b.- Título del gráfico.
c.- Cuerpo del gráfico o gráfico propiamente dicho (incluye la clave o leyenda de ser necesaria esta).
d.- Pie del gráfico.Las características de estos componentes, salvo el gráfico propiamente dicho, son las mismas de dichos componentes en la tabla o cuadro estadístico, así que no insistiremos en ellas y pasaremos directamente a discutir la construcción de los diferentes tipos de gráficos.
Debemos hacer una aclaración antes de continuar. En la actualidad es muy infrecuente encontrar un gráfico hecho a mano. Generalmente se emplean sistemas graficadores de microcomputadoras. Esto no invalida la necesidad de conocer las reglas y convenciones establecidas con respecto a la confección de los mismos. Dada la enorme libertad que brindan algunos de esos sistemas, en más de una oportunidad hemos visto gráficos confeccionados por estos medios que presentan errores, entre otras cosas, por seleccionar un tipo de gráfico no adecuado para la información que se desea representar (4, 5).
3.- Diferentes tipos de gráficos.
Se usa fundamentalmente para representar distribuciones de frecuencias de una variable cualitativa o cuantitativa discreta y, ocasionalmente, en la representación de series cronológicas o históricas. Uno de los ejes sirve para inscribir las frecuencias, ya sean absolutas o relativas (%), y el otro para la escala de clasificación utilizada. Un ejemplo de este tipo de gráfico es el que se presenta a continuación:
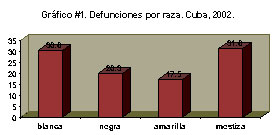
Cada clase se representa con una barra o rectángulo cuya altura (si el eje de frecuencias es el vertical) resulta proporcional a la frecuencia que representa. Todas las barras deben tener el mismo grosor y el espacio entre barras debe ser el mismo, teniendo un ancho de 0,5 a 1 vez el de las barras.
El orden de las barras en el gráfico debe ser el mismo que en la tabla que le sirve de fuente. Por ello, si no existe un criterio 'a priori' de orden entre las clases establecidas, pueden ordenarse las mismas (y, como es lógico, las barras en el gráfico) en orden ascendente o descendente de las frecuencias, para facilitar la interpretación de esos resultados.
b) Gráfico circular, de sectores o pastel.
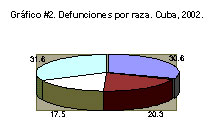
El gráfico siguiente es un ejemplo típico de gráfico circular (confeccionado con los mismos valores del gráfico anterior):
Se usa, fundamentalmente, para representar distribuciones de frecuencias relativas (%) de una variable cualitativa o cuantitativa discreta. En este gráfico se hace corresponder la medida del ángulo de cada sector con la frecuencia correspondiente a la clase en cuestión. Si los 360º del círculo representan el 100 % de los datos clasificados, a cada 1% le corresponderán 3,6º. Luego, para obtener el tamaño del ángulo para un sector dado bastaría con multiplicar el por ciento correspondiente por 3,6º (por simple regla de tres).
Mediante un sector circular se representan las medidas angulares correspondientes a las diferentes categorías, respetando el orden establecido en la tabla, partiendo de un punto dado de la circunferencia. Ese punto dado generalmente es el punto más alto de la circunferencia (12 en el reloj). Si lo que se representa en cada sector no puede colocarse dentro del mismo, se elabora una leyenda o se coloca fuera, adyacente al mismo. Se acostumbra a diferenciar los sectores con tramas o colores diferentes, lo que hace que resulte un gráfico más vistoso que el de barras simples.
c) Gráfico de barras múltiples.
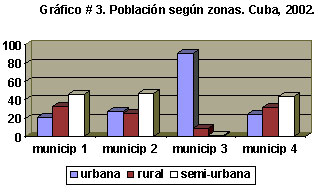
Se usa para representar las frecuencias observadas en clasificaciones dobles, es decir, cuando son dos los criterios de clasificación, para variables cualitativas o cuantitativas discretas. Su forma de construcción es similar a la del gráfico de barras simples, sólo que en este caso se representan dos variables. El hecho de ser doble, triple, cuádruple, etc., parte del número de clases que tenga la variable, que no es el criterio principal de clasificación. Las barras que integran una barra múltiple se colocan juntas o ligeramente solapadas.Veamos un ejemplo de este tipo de gráfico:
Este es un gráfico de barras triples. En la leyenda aparece el criterio de clasificación que complementa al que aparece en el eje de categorías. Note la separación entre los “tríos” de barras.
d) Gráfico de barras compuestas.
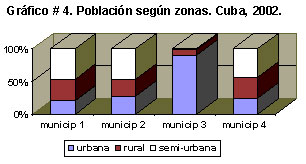
Su objetivo es la representación de las frecuencias relativas (%) observadas en clasificaciones dobles, es decir, cuando son dos los criterios de clasificación, para variables cualitativas o cuantitativas discretas.
Su forma de construcción es la siguiente: cada barra representa el 100 % de los individuos en cada clase del criterio principal de clasificación y se divide, proporcionalmente, en los por cientos correspondientes a las clases del otro criterio de clasificación. Como es lógico, las diferentes partes en que se dividen las barras compuestas se diferencian con tramas o colores diferentes.
Este gráfico se usa para representar una distribución de frecuencias de una variable cuantitativa continua.
Habitualmente se representa la frecuencia observada en el eje Y, y en el eje X la variable. La escala del eje correspondiente a la variable se rotula con los límites inferiores de notación de las clases consideradas y se agrega al final el que le correspondería a una clase subsiguiente inexistente. En este caso, las frecuencias deben resultar proporcionales no a la altura de las barras, sino al área de las mismas, lo que significa que la obtención de las alturas de las barras resulta un poco más compleja que en los gráficos anteriores. Además, las barras van contiguas y no separadas, por la naturaleza continua de la variable de clasificación.
Para lograr la proporcionalidad entre la frecuencia y el área de la barra que esta representa el procedimiento es el siguiente: sabemos que el área de un rectángulo es el producto de la base por la altura y que la base de una barra en el gráfico es, precisamente, la amplitud del intervalo de clase, luego la formulación de esa 'proporcionalidad' sería:
frecuencia observada = amplitud del intervalo* altura de la barra
Conocemos la frecuencia observada y la amplitud de cada uno de los intervalos, por tanto, para calcular las alturas de las barras sólo se tendría que despejar en la fórmula correspondiente, lo que quedaría:
altura de la barra = frecuencia observada / amplitud del intervalo
Debido a la forma de obtención de esas alturas, el eje de las frecuencias debe rotularse como número de individuos por unidad de medida de la variable en cuestión, por ejemplo: 'defunciones por año de edad'; 'número de individuos por kg de peso; etc.
El procedimiento que hemos explicado es el general, pero sucede, en el caso particular de que las amplitudes de todos los intervalos de clase sean iguales, que no es estrictamente necesario realizar estos cálculos: sería dividir todas las frecuencias por una constante y eso no alteraría el gráfico, pues se mantendría la misma relación de proporcionalidad entre las frecuencias.
Veámoslo a través de un ejemplo, cuando las amplitudes de los intervalos son iguales:
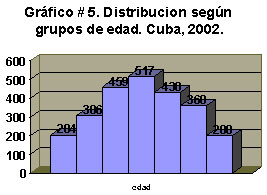
En este caso se usó la frecuencia absoluta como altura de la barra. Todas las barras tienen el mismo ancho y van unidas, una a continuación de la otra, porque están representando una variable continua (edad).
Es sencillo darse cuenta de que es imposible presentar otra distribución en ese gráfico, pues unas barras podrían ocultar a otras. Es decir, este tipo de gráfico sólo es útil para presentar una distribución.
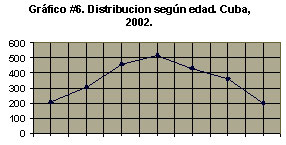
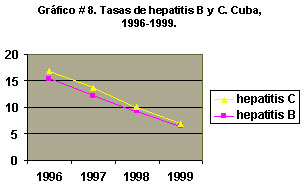
Se utiliza, al igual que el histograma, para representar distribuciones de frecuencias de variables cuantitativas continuas, pero como no se utilizan barras en su confección sino segmentos de recta, de ahí el nombre de polígono. Habitualmente se usa cuando se quiere mostrar en el mismo gráfico más de una distribución o una clasificación cruzada de una variable cuantitativa continua con una cualitativa o cuantitativa discreta, ya que por la forma de construcción del histograma sólo se puede representar una distribución.
Para su confección, una vez construidas y rotuladas las escalas, de manera similar a como se realiza para un histograma, los valores de alturas obtenidos se plotean sobre el punto medio o marca de clase de los intervalos correspondientes y luego se procede a unir esos puntos con segmentos de recta.
Veamos un ejemplo de polígono de frecuencias:
g) Gráfico de frecuencias acumuladas u ojiva.
Su objetivo, al igual que el histograma y el polígono de frecuencias es representar distribuciones de frecuencias de variables cuantitativas continuas, pero sólo para frecuencias acumuladas.
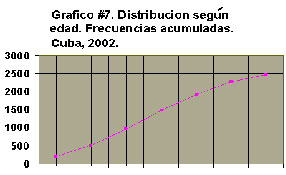
No se utilizan barras en su confección, sino segmentos de recta, por ello no sólo es útil para representar una distribución de frecuencias sino también cuando se quiere mostrar más de una distribución o una clasificación cruzada de una variable cuantitativa continua con una cualitativa o cuantitativa discreta. Este es un ejemplo de una ojiva:
La diferencia con el polígono de frecuencia es que la frecuencia acumulada no se plotea sobre el punto medio de la clase, sino al final de la misma, ya que representa el número de individuos acumulados hasta esa clase. Como el valor de la frecuencia acumulada es mayor a medida que avanzamos en la distribución, la poligonal que se obtiene siempre va a ser creciente y esa forma particular de la misma es la que ha hecho que se le dé también el nombre de ojiva.
Este es uno de los más sencillos de confeccionar. Su uso estadístico fundamental es en la representación de series cronológicas, y en casos particulares, como el del Crecimiento y Desarrollo Humanos, para representar los valores promedio o posicionales (medias, medianas y percentiles, que se estudiarán más adelante) de muchas dimensiones: peso para la edad, peso para la talla y talla para la edad, entre otras.
Uno de los ejes (habitualmente el horizontal) se usa para la unidad de tiempo estudiada: años, días, etc.. En el otro eje se representa la frecuencia o el indicador calculado a partir de esos datos. En este tipo de gráfico es particularmente importante la relación de proporcionalidad entre los ejes para evitar malas interpretaciones del fenómeno que se presenta.
El gráfico que sigue es un ejemplo de gráfico de este tipo:
En el mismo gráfico se puede presentar más de una serie de datos si la escala usada se adecua para todas, cuando los valores de las mismas no son extremadamente diferentes.
4.- Errores más comunes en la confección de gráficos.
En la confección de un gráfico se pueden cometer dos tipos de errores: errores de forma y errores de contenido. Aquí mencionaremos los que se han observado con más frecuencia en las publicaciones científicas.
De forma:
· No uso de la identificación.
· No aparición de título o títulos extremadamente extensos.
· Títulos que no responden a las preguntas básicas.
· Gráficos muy cargados y/o sumamente complejos de interpretar.
· Desproporción notable entre las longitudes de los ejes.
· Omisión de los rótulos de los ejes y/o las unidades de medida.De contenido:
· Uso de gráficos inadecuados dada la naturaleza de lo que se representa.
· Omisión de la leyenda donde se han usado claves o símbolos.
· No respetar alguna de las reglas establecidas para la construcción del gráfico en particular. Por ejemplo, barras unidas cuando se trabaja con variable cualitativa o discreta.5.- Otros tipos de representación gráfica.
Existen muchos otros tipos de gráficos con propósitos más específicos que los discutidos anteriormente. Daremos una visión muy general de los mismos sin adentrarnos en las particularidades relativas a la construcción. Estos son gráficos en los que, en lugar de tener escalas aritméticas en los dos ejes de coordenadas (como es el caso del gráfico aritmético simple), uno de los ejes tiene una escala especial. Esos gráficos reciben los nombres de la escala especial, no aritmética. Por ejemplo:- gráfico semilogarítmico (una escala logarítmica)
- gráfico probabilístico (una escala probabilística)
- gráfico logístico (una escala logística)Veamos la forma más frecuente de uso de uno de ellos.
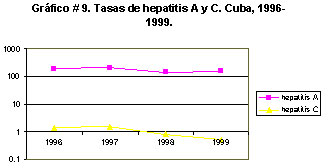
Semilogarítmico: En ocasiones, al representar series cronológicas para comparar, resulta que los valores de las diferentes series pueden diferir grandemente y eso hace prácticamente imposible el uso del Grafico aritmético simple, pues deben aparecer en la escala del eje Y valores que pueden estar 'muy distantes' entre sí. La solución es usar una escala logarítmica en dicho eje y así pueden colocarse todos los datos sin alterar seriamente sus comportamientos, de modo tal que las comparaciones sean válidas. Veámoslo con un ejemplo:
El eje correspondiente a las tasas es un eje logarítmico, para poder representar números de magnitudes tan diferentes al unísono.
También hay formas de presentación gráfica que no son gráficos propiamente dichos. Al menos, no de los tipos que hemos visto. Esas presentaciones pueden ser:
- Mapas con localizaciones específicas dando información sobre el tema de que se trate. Por ejemplo, dando colores o intensidades diferentes a las distintas zonas geográficas en función del grado de afectación por el fenómeno en estudio.
- Fotos.
- Esquemas.
- Organigramas, etc.
Nota complementaria: Sobre los gráficos basados en barras (barras simples, múltiples, etc) existe la prohibición de “cortar” el eje de las frecuencias (número de casos, por cientos, etc). Para el resto se autoriza el “corte” de cualesquiera de los ejes, siempre y cuando este no interrumpa el trazado. Esto nos ayuda a reducir el gráfico sólo al área del sistema de ejes coordenados entre cuyos valores se mueven los datos a graficar.
1-Los gráficos se reciben con agrado por parte de los editores y lectores, pero la apariencia es lo menos importante, el objetivo de la presentación gráfica es mejorar la presentación del contenido científico.
2-Si el contenido de los resultados se puede hacer de forma textual, no se recomienda la presentación gráfica, ya que eleva los costos de publicación.
3- El objetivo básico de un gráfico es transmitir la información de forma tal que pueda ser captada rápidamente, de un golpe de vista, un gráfico debe ser ante todo sencillo y claro, a pesar de su aspecto artístico, ya que se elabora para ser incluido en un trabajo científico.
1-Huth EJ. Medical Style and Format: an International Manual for Authors, Editors, and Publishers. Philadelphia: ISI Pr; 1997.
2-CBE Style Manual Committee. CBE Style Manual. 5th ed. Bethesda, MD: Council of Biology Editors; 1993.
3-Iverson C, Dan BB, Glitman P, Jogel B, Jasson N, Bacall J, et al. American Medical Association Manual of Style. 8th ed. Baltimore: Williams & wilkins; 1999.
4-Reynolds L, Simmonds D. Presentation of Data in Science. Dordrecht: Martinus Nijhoff; 1984.
5-Scientific Illustration Committee. Illustrating Science: Standards for Publication Bethesda, Md: Council of Biology Editors; 1988.