Estudio de la Variabilidad de la Frecuencia Cardiaca Mediante
el Análisis de recurrencia Visual.
<Resumen><Introducción> <Material y Métodos><Resultados><Discusión>
<Conclusiones><Referencias>
Autores:
Rolando Hong Enríquez
Luis García Domínguez
Miguel Sautié Castellanos
José Luis Hernández CáceresDirecciones: Centro de Cibernética Aplicada a la Medicina (CECAM).
Instituto Superior de Ciencias Médicas de la Habana (ISCM-H).
Calle 146 esquina a 31; # 2511, Cubanacán, Playa, Ciudad Habana, CP 10400, Cuba.
Teléfono: (537) 2711354
Instituto Cubano de Arte e Industria Cinematográficos (ICAIC). Calle 23 entre 10 y 12. Vedado. Ciudad de la Habana, Cuba.
Teléfono: (537) 552851La correspondencia debe dirigirse a:
Rolando Hong Enríquez
E-mail: hong@cecam.sld.cu
Institución:
Centro de Cibernética Aplicada a la Medicina
Se aplicaron varios métodos relacionados con la implementación del análisis de recurrencia visual a un grupo de 10 registros de señales RR obtenidas a partir de una señal de RR de 24 horas de duración de un sujeto sano voluntario del sexo masculino. En particular la utilización de la función de información mutua y del método de los falsos vecinos mostraron que la señal posee una elevada dimensión de inmersión , por esta razón se descarta la posibilidad de que la señal posea una dinámica de caos clásico. Esto está en correspondencia con resultados ya alcanzados en la literatura [14]. En general, en los gráficos de recurrencia se aprecia la presencia de cierta estructura en las señales RR estudiadas, este resultado se confirma con las mediciones de entropía espacio-temporal (aproximadamente 50% para todas las señales observadas). Conclusiones: i) consideramos que el análisis de recurrencia visual puede ser una herramienta util para explorar la estructura de las señales de variabilidad de la frecuencia cardíaca y su posible alteracion en algunas enfermedades.
Palabras claves: Variabilidad de la frecuencia cardíaca, análisis de recurrencia visual, método de los falsos vecinos, método de información mutua, caos clásico, entropía espacio-temporal.
Abstract: We applied various methods related with the implementation of visual recurrence analysis to a group of 10 RR signals obtained from a larger 24 hour RR signal of a healthy male volunteer; in particular, the use of the mutual information function and the method of false nearest neighbors showed that the RR signal has a very high embedding dimension , this result dismiss the possibility for the system dynamics been governed by classical chaos which is in perfect agreement with a previous work [14]. In general the recurrence plots shown the presence of some degree of structure in the RR signals studied, which is confirmed by the values of spatio-temporal entropy (approximately 50% for all the signals). Conclusions i) The visual recurrence analysis can be used only as an exploratory tool to determine the degree of ‘structure’ present in heart rate variability signals.
Key Words: Heart Rate Variability, Visual Recurrence Analysis, False nearest neighbors, Mutual Information, Classical chaos, spatio-temporal entropy.
INTRODUCCIONEl estudio de la variabilidad de la frecuencia cardíaca (VFC) ha ocupado un lugar importante en la literatura durante los últimos años [1-5]. En particular, se ha escogido la duración de los cardio-intervalos (intervalos RR) como una de las señales derivadas del electrocardiograma más representativas de dicha variabilidad. Sorprendentemente, las series de intervalos RR han mostrado poseer una estructura bastante compleja, discutiéndose la posibilidad de que esta señal pueda ser gobernada por un régimen caótico, esto último ha sido fuente de una gran controversia en la literatura [6,7].
Para responder a este tipo de interrogante sobre la naturaleza de la VFC se han empleado numerosas herramientas tomadas en su mayor parte del análisis de series de tiempo [8]. La teoría de los sistemas dinámicos no lineales brinda muchos métodos para la identificación y clasificación de los patrones dinámicos en una serie de tiempo observada. Debido a que los sistemas vivos están caracterizados por estructuras biológicas estables que se encuentran lejos del equilibrio, tales métodos pueden ser utilizados para caracterizar estos sistemas [9,10]. El análisis de recurrencia visual [13] es una de estas herramientas.
La mayor parte de los análisis se llevaron a cabo mediante el programa Vra (v 4.2) . Para el procesamiento se utilizó un registro de electrocardiograma de 24 horas de duración de un voluntario sano de sexo masculino. Para el análisis solo utilizamos 10 segmentos de esta señal con 8000 puntos cada uno tomados desde el principio del registro de 24 horas y con un solapamiento consecutivo del 50%.
Sobre estos segmentos se aplicaron los métodos siguientes.
Función de información mutua
La información mutua estima el valor óptimo del tiempo de retardo ( T ) para la reconstrucción del espacio de fases. Los detalles de esta técnica se pueden encontrar en [11]; la idea general es que un buen tiempo de retardo T es aquel que dado un estado del sistema X(t) provea una información nueva máxima acerca del estado X (t + T), la diferencia entre el estado real y el predicho para X (t + T) da una medida de esta información. Muchos bits de información pueden ser predichos para ( T )pequeña (los estados se encuentran cerca), pero esta cantidad de bits debe ir disminuyendo a medida que ( T ) aumenta, de esta manera se toma como óptimo aquel donde se encuentre el primer mínimo local de la función de información.
Método de los falsos vecinos cercanos.
La base teórica del método es que para los sistemas determinísticos, los puntos cercanos en el espacio de fases reconstruido permanecen de esta forma en espacios de mayor dimensión; esto es cierto si la dimensión de inmersión es suficientemente elevada como para resolver el determinismo [12].
Basado en esto el algoritmo funciona de la siguiente manera: Dado un punto en m dimensiones, se buscan sus puntos vecinos más cercanos . Dejemos que la distancia entre y sea ; si la distancia entre estos puntos en el espacio de dimensión m + 1 es mayor que ( es un determinado factor) entonces el punto se marca como un falso vecino cercano. La fracción de falsos vecinos cercanos indica entonces si el proceso es determinístico en m dimensiones o no. Si m es mayor que el número de grados de libertad activos esta fracción debe ser cero o al menos muy pequeña, y no debe ser cero en cualquier otro caso.
Gráficos de recurrencia
En el análisis de recurrencia visual [13] una serie de tiempo unidimensional de un fichero de datos es expandida en un espacio de alta dimensión en el cual ocurre la dinámica que genera al proceso. Esto se hace utilizando una técnica llamada ‘inmersión en coordenadas de retraso’, la cual crea un retrato del espacio de fases del sistema dinámico bajo estudio que es topológicamente equivalente al sistema original [15]. Para expandir una señal unidimensional en un espacio de fases m-dimensional se sustituye cada observación en la señal original con el vector:Donde
T = tiempo de retardo
m = dimensión de inmersiónUn gráfico de recurrencia visual se realiza calculando todas las distancias Euclidianas entre cada par de vectores en este espacio m-dimensional, a la matriz obtenida se le asigna un código de colores y se representa en dos dimensiones.
Entropía espacio-temporal
La entropía espacio-temporal es un estimador de la ‘cantidad de estructura’ de una imagen tanto en el dominio del tiempo como en el dominio del espacio. Esencialmente, esta medida compara la distribución global de los colores sobre todo el gráfico de recurrencia con la distribución de colores sobre cada línea diagonal de este mismo gráfico. En términos físicos, esta cantidad compara la distribución de las distancias entre todos los pares de vectores en el espacio de fases reconstruido con la distribución de las distancias entre diferentes órbitas que evolucionan en el tiempo. El resultado es normalizado y presentado como porciento de ‘máxima’ entropía.
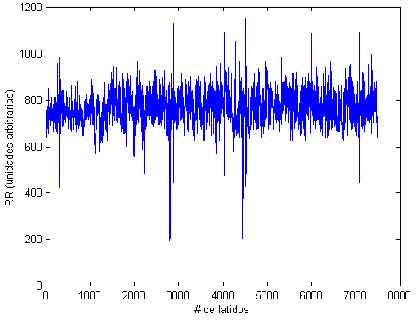
RESULTADOSEn la figura 1 puede apreciarse una señal típica de variabilidad de frecuencia cardiaca (intervalos RR) para algo mas de 7000 latidos del corazón. La forma irregular de la señal puede sugerir lo difícil que resulta extraer información relevante a partir de la misma.
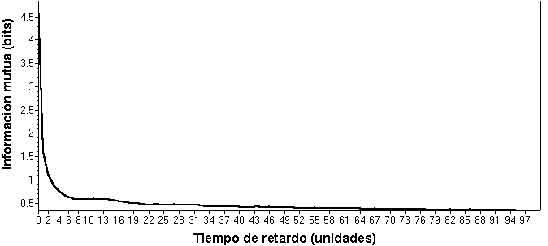
Figura 1. Señal de intervalos RR que representa la variabilidad de la frecuencia cardiaca.La estimación del tiempo de retardo ( T ) de la señal mediante la función de información mutua mostró una gran homogeneidad para los registros estudiados encontrándose T = 4 ó T = 5 en todos los casos. Un resultado típico se aprecia en la figura 2; nótese que la función posee un mínimo local alrededor de T = 5, con este valor de ( T ) se procede a la utilización del método de los falsos vecinos cercanos.
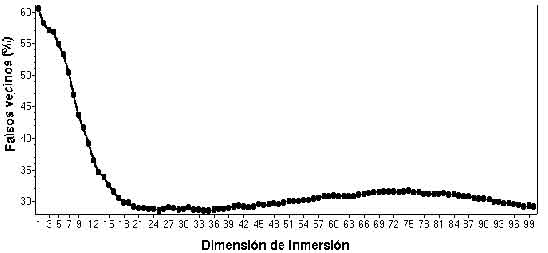
Figura 2. Función de información mutua. Puede verse que el primer mínimo local se observa aproximadamente alrededor de T = 5, por tanto este es el valor elegido para el tiempo de retardo.La dimensión de inmersión fue igualmente elevada para cada uno de los registros, con en todos los casos y con 8% de falsos vecinos en el mejor de los casos, [lo cual asegura un atractor de muy alta dimensión en cualquiera de los casos]. Véase en la figura 3 el resultado del método de los falsos vecinos cercanos cuyos resultados de tiempo de retardo (T = 5) se mostró en la figura 2; la dimensión de inmersión global óptima fue de m = 95 para un 10% de falsos vecinos en este caso en particular.
Figura 3. Método de los falsos vecinos cercanos. Función de información mutua. Puede verse que el porciento de falsos vecinos alcanza un mínimo alrededor m = 30 de aunque vuelve a disminuir alrededor de m = 90.Para el caso de los gráficos de recurrencia es útil mostrar a modo de comparación los resultados obtenidos para datos altamente aleatorizados como el ruido blanco y para una función altamente estructurada como la función y = seno (x), ambos casos se aprecian en las figuras 4 y 5 respectivamente. Véase claramente la diferencia entre los gráficos de datos estructurados y no estructurados.
Figura 4. Gráfico de recurrencia para una señal de ruido blanco. Véase la ausencia de cualquier patrón reconocible.
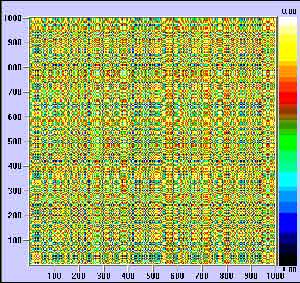
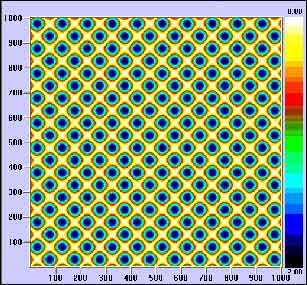
Figura 5. Gráfico de recurrencia para una señal y = seno (x). Véase el ‘orden’ asociado a una sinusoidal perfecta.Finalmente la figura 6 muestra el gráfico de recurrencia para una señal RR. Observe que esta figura posee una apariencia intermedia con respecto a las mostradas en las figuras 4 y 5, lo cual demuestra la presencia de ‘cierto orden’ en los datos, esto queda confirmado con el cálculo de la entropía espacio-temporal que en este caso específico fue del 49% y en total se mantuvo en un rango de 42-53% para el resto de los registros.
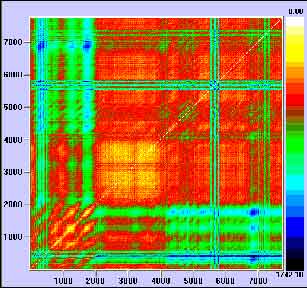
Figura 6. Gráfico de recurrencia para la señal asociada a la variabilidad de la frecuencia cardiaca mostrada en la figura 1. El ‘orden’ de esta señal claramente se encuentra en niveles intermedios a lo mostrado en las figuras 4 y 5. Una forma de cuantificar este orden es a través de la entropía espacio-temporal.
Los métodos actuales de análisis de series de tiempo si bien representan una aproximación diferente al análisis de señales con respecto a técnicas más clásicas como el análisis espectral, no debe dejarse de señalar que aún poseen imperfecciones técnicas, en particular se ha discutido exhaustivamente la imposibilidad de obtener señales que cumplan rigurosamente con los requisitos del teorema de Takens [16]. Otro aspecto a tomar en consideración el la pobre estabilidad de los algoritmos ante la longitud de la señal y la presencia de ruido en esta [17].
Dentro de la teoría de los sistemas dinámicos se ha prestado especial atención a la descripción del caos clásico; este ha sido muy estudiado sobre todo en sistemas de ecuaciones diferenciales y de ecuaciones en diferencias que son hoy sistemas clásicos en la literatura dentro del tema [8]. No es sin embargo trivial la tarea de demostrar que datos reales obtenidos a partir de la experimentación estan regidos por este tipo de dinámica; este ha sido el caso de la VFC [6]. En este sentido tal problema no se aborda de modo exhaustivo en el presente trabajo, no obstante, los estimados de la dimensión de inmersión ( m )muestran fuertes evidencias de que la dinámica de la serie de intervalos RR no está gobernada por un sistema de caos clásico, puesto que se encontraron valores elevados para todos los casos incluso cuando en nuestros cálculos el porciento de falsos vecinos no fue inferior al 8% para ningún registro, valor muy superior al 1% recomendado en la literatura pero que es suficiente para desechar la hipótesis de caos clásico; este resultado concuerda con el encontrado por algunos autores [7,14]. Debe no obstante notarse que en la estimación de la dimensión de inmersión muchas veces se observa un mínimo local alrededor de la dimensión m = 30, creemos que este es un valor más probable para la dimensión de inmersión, pero incluso con este valor creemos incorrecto seguir apoyando la idea de caos clásico en la señal RR y la variación en los patrones de recurrencia no varían de manera realmente apreciable como para hacer cambiar nuestro punto de vista.
Queda aún la posibilidad de que pueda tratarse de caos de alta dimensión, sin embargo, este tipo de sistema no ha despertado gran interés en la literatura. La hipótesis de caos de alta dimensión para la VFC posee más sentido fisiológico, pues es poco probable que el número de mecanismos reguladores del sistema cardiovascular sea bajo y por tanto representable mediante una dinámica de caos clásico.
La hipótesis de caos de alta dimensión afronta grandes problemas en su comprobación experimental, pues además de las restricciones teóricas asociadas con la dificultad de diferenciar el ‘caos’ del ruido a muy alta dimensión, se encuentra también la dificultad asociada con modelos excesivamente complicados con un numero de parámetros muy elevado.
Es valido sin embargo señalar que es poco probable que el método de estimación de la dimensión de inmersión a través de los falsos vecinos sea capaz de clasificar correctamente al caos de alta dimensión, en particular, creemos que la variación, observada en la figura 3 a partir de una dimensión mayor que 30 se debe fundamentalmente a que para esos valores la influencia del ruido se hace notar y el método comienza a perder sensibilidad. Existe al menos un trabajo [18]que hace alusión a una posible implicación de los gráficos de recurrencia como posible herramienta para determinar parámetros clínicamente relevantes en la señal de la variabilidad de la frecuencia cardiaca; sin embargo no se hace ningún estudio previo de la señal y prácticamente ‘se asume’ que la dimensión de inmersión de la señal es m = 5, nuestros resultados no concuerdan con tal punto de vista y por tanto creemos que las conclusiones extraídas a partir de estos estimados no están plenamente justificadas.
El análisis de recurrencia visual puede brindar una médica cualitativa del grado de ‘orden’ en las señales de variabilidad de la frecuencia cardíaca, pero dada la dificultad teórica existente en la diferenciación de ‘caos’ y ruido, creemos que quizás el método deba combinarse con otras medidas cuantitativas o si es posible, derivar medidas informativas a partir de los gráficos de recurrencia. Con tal enfoque, un estudio clinico exaustivo podria brindar buenos resultados.
Parece poco probable que las señales de variabilidad de la frecuencia cardiaca estén gobernadas por un sistema de caos clásico de baja dimensión aunque esta posibilidad no queda completamente descartada debido a la inevitable presencia de ruido en los registros.
1. Suder K., Drepper F.R., Scheik M., Hnas-Henning A. One-dimensional, nonlinear determinism characterizes heart rate pattern during paced respiration. Am. J. Physiol. 275 (44): H1092-H1102, 1998
2. Mäkikallio T.H., Høiber S., Køber L., Torp-Pedersen C., Peng C., Goldberger A.L., Huikuri H.V.
3. Fractal analysis of heart rate dynamics as a predictor of mortality in patients with depressed left ventricular function after acute myocardial infarction. Am. J. Cardiol, 83:836-839, 1999.
4. Sakata S., Hayano J., Mukai S., Okada A., Fujinami T. Aging and spectral characteristics of the nonharmonic component of 24-h heart rate variability. Am. J. Physiol. 276(45):R1724-R1731, 1999.
5. Peng C.K., Havlin S., Stanley H.E., Goldberger A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 5:82-87, 1995.
6. Bigger J.T., Steinman R.C., Rolnitzki L.M., Fleiss J.L., Albrecht P., Cohen R.J. Power law behavior of RR interval variability in healthy middle aged persons, patients with recent acute myocardial infarction, and patients with heart transplants. Circulation 93:2142-2151, 1996.
7. Goldberger A. Is normal heartbeat chaotic or homostatic?. News Physiol. Sci. 6:87-91, 1991.
8. Kanters J.K., Holstein-Rathlou N.H., Agner E. Lack of evidence for low dimensional chaos in heart rate variability. Journal of Cardiovascular Electrophysiology 5(7):591-601, 1994.
9. Bergé P, Pomeau Y., Vidal C. Order within chaos. John Wiley & Sons, New York,1-350, 1984.
10. Drepper F.R., Engbert R., Stollnewerk N. Nonlinear time series analysis of empirical population dynamics. Ecol. Modell. 75/76:171-181, 1994-11-06
11. Glass L., Mackey M.C. From flocks to chaos. Princeton, N.J.: Princeton University Press, 1988.
12. Fraser A., Swinney H.L.Independent coordinates for strange attractors from mutual information. Phys. Rev. A 33 (1986) pp. 1134-1140.
13. Kennel M.B., Brown R., Abarbanel H.D.I., Determining embedding dimension for phase space reconstruction using a geometrical construction. Phys. Rev. A 45, 3403, 1992
J.P. Eckmann, S. Oliffson Kamphorst and D. Ruelle Recurrence plots of dynamical systems.1987, Europhys. Lett., Vol. 4, No. 9, pp. 973-977
14. JL Hernández, L. García, Guido Enzmann, A. García. La regulación autonómica del intervalo cardiaco como un sistema no linear estocástico con múltiples atractores. Revista CENIC Ciencias Biológicas 30(3):180-186, 1999
15. Takens F. Detecting strange atractors in turbulence, in: D.A. Rand, L.S. Young (Eds.). Dynamical systems and turbulence, vol 898, Springer, Berlin, 1981: 365-381-
16. Noakes L, The Takens Embedding theorem Int. J. of Bifurcation and Chaos 1991 1: 867-872
17. Galka A, Maab T, Pfister G Estimating the dimensions of high dimensional attractors: a comparison between two algorithms Physica D 1998 121: 237-251
18.Veroneckas J, Ulbikas J, Cenys A, Žemaityté D Non-linear dynamics of heart rate during individual sleep stages. First Virtual Congress of Heart Rate Variability. September 10, 2001. (http://www.hrvcongress.org )