tComplejidad y codificación en RNAs no codificadores.
<Resumen> <Introducción><Materiales y Métodos>t<Resultados y Discusión>
<Conclusiones> <Agradecimientos> <Bibliografía>
Autores:
Luis García Domínguez *
Rolando Hong Enríquez **
Miguel Sautié Castellanos **
José Luis Hernández Cáceres **
Direcciones:
* Instituto Cubano de Arte e Industria Cinematográficos (ICAIC). Calle 23 entre 10 y 12. Vedado. Ciudad de La Habana, Cuba.
Teléfono: (537) 552851
** Centro de Cibernética Aplicada a la Medicina (CECAM). Instituto Superior de Ciencias Médicas de La Habana (ISCM-H).
Calle 146 esquina a 31; # 2511, Cubanacán, Playa, Ciudad Habana, C.P. 10400, Cuba.
Teléfono: (537) 2711354
Email: hong@cecam.sld.cu
La estructura de la información presente en las regiones genéticas no codificadoras aún está muy poco caracterizada. En este trabajo se plantea como objetivo fundamental hacer una recodificación de estas secuencias y utilizar medidas teórico-informacionales de análisis, como la entropía de Shannon y la complejidad de Lempel-Ziv, para caracterizar estos datos. La complejidad de Lempel-Ziv mostró un patrón similar no aleatorio en secuencias no codificadoras de diferentes organismos; con medidas derivadas de la entropía de Shannon se obtuvieron evidencias de patrones que hacen posible un tipo de codificación diferente al código de tripletes clásico planteado para secuencias codificadoras.
Palabras claves: regiones no codificadoras, Entropía de Shannon, Complejidad LZ.
INTRODUCCIÓN:La automatización de las técnicas de la biología molecular ha traído consigo un incremento notable en el volumen de información de origen genético con el que actualmente cuentan los investigadores de todo el mundo. Sin embargo, el contenido informacional de gran parte de estas secuencias es en su mayor parte desconocido; en particular, las secuencias no codificadoras han mostrado ser difíciles de interpretar [1] y los estudios que las incluyen solo son capaces de mostrar sin margen de dudas una correlación a largo plazo mediante la presencia de un proceso 1/f [2], aunque existen evidencias de otras regularidades [3]. Sin embargo, estos resultados se han obtenido con secuencias genéticas extremadamente largas donde se analizan de conjunto intrones, exones y otras regiones funcionales del material genético.
En este trabajo pretendemos mostrar los resultados de nuestra primera aproximación a estos problemas. Hemos usado como herramientas la entropía de Shannon [4] y la medida de complejidad para secuencias de Lempel-Ziv [5]. Combinando estos métodos con recodificaciones sencillas de las secuencias genéticas hemos podido encontrar algunas regularidades.
MATERIALES Y MÉTODOS:Datos
Todas las secuencias analizadas en el presente estudio fueron obtenidas a partir de una base de datos de secuencias no codificadoras de ácido ribonucleico (RNA). Puede accederse a estos datos a través de Internet [6].
Algoritmo de complejidad de Lempel-Ziv.
Uno de los aspectos teóricos más profundamente estudiados en las ciencias modernas ha sido la formalización del término 'complejidad'; de hecho se han presentado poco mas de 30 definiciones matemáticas que describen este concepto [7, 8]. Entre estas definiciones, el algoritmo de Lempel-Ziv ha mostrado ser particularmente útil para el análisis de secuencias. Este algoritmo, también conocido como complejidad LZ, mide el número de patrones distintos que deben ser copiados para reproducir una secuencia dada. Descrito brevemente, en este algoritmo una secuencia S = s
1s2s3.....snes recorrida de izquierda a derecha, y cada vez que se encuentra una subsecuencia nueva, se incrementa un contador de complejidad c (S). Al terminarse la secuencia S, el número resultante c (S) es la medida de complejidad para la cadena S. El valor calculado se divide entre el tamaño de la secuencia. Para una misma secuencia este procedimiento se repite tomando segmentos cada vez mayores de la secuencia, partiendo siempre del primer elemento de la misma.Sin embargo, para que el análisis sea completo, debe notarse que solo tienen sentido los valores relativos de c (S); en particular es muy informativa la comparación de c (S) de la secuencia original, con el valor de complejidad obtenido a partir de la secuencia aleatoria correspondiente. Otros detalles y teoremas relacionados con este método pueden encontrarse en el articulo de Lempel y Ziv de 1976 [5].
Entropía de Shannon.
Shannon, en la década del 40, introduce una medida relacionada con todos los estados posibles de una fuente de información dada [4]. La entropía de Shannon se podría definir como una medida de incertidumbre promedio, la cual se calcula a partir de la probabilidad de ocurrencia de cada una de las letras de un alfabeto de acuerdo con la siguiente fórmula:
(a)
El número total de símbolos posibles a utilizar en la fórmula (a) varía en cada codificación. Tomándose secuencias genéticas de longitud n, tendremos 4n posibles símbolos en cada codificación. En lo sucesivo denominaremos a n, orden de la codificación. A partir de los valores de frecuencia de símbolos se calcula la entropía de las secuencias genéticas por cada orden de codificación (Hab(n)). Este mismo procedimiento se sigue para la versión aleatorizada de la secuencia no codificadora original y se obtienen de esta forma los valores relativos (Hrel(n)). Le llamaremos al cociente (Hab(n)/Hrel(n)) entropía normalizada.
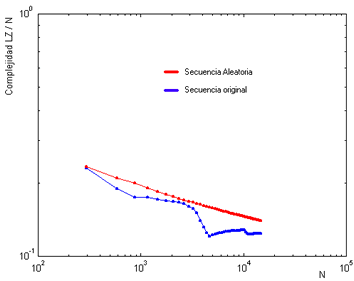
La figura 1 muestra el gráfico log-log de complejidad LZ vs. tamaño de una secuencia no codificadora. Es evidente la diferencia con respecto a la secuencia aleatoria correspondiente. Resultados similares fueron obtenidos para secuencias codificadoras y no codificadoras de diferentes organismos (datos no mostrados).
Figura 1. Complejidad de Lempel-Ziv para varios tamaños de la secuencia analizada (N). Obsérvese las diferencias entre la secuencia original y los de su cadena aleatoria correspondiente.La dificultad para encontrar regularidades a corto plazo en secuencias de ADN, aún cuando se utilizan secuencias codificadoras de gran tamaño, es un problema que no está resuelto de manera satisfactoria. Creemos que los fracasos en esta área se deben, al menos en parte, a que no se ha tenido en cuenta la posibilidad de que hacer codificaciones radicalmente diferentes del material genético, pero evidentemente tampoco han aparecido en la literatura métodos adecuados.
La figura 2 muestra la entropía de Shannon normalizada vs. Orden de codificación de una secuencia codificadora y una no codificadora. La preferencia por los valores 3 y 6 puede tener su origen en el clásico código de tripletes del ADN para la secuencia codificadora. A pesar de existir un valor mínimo de
para la secuencia no codificadora, este solo hecho no es suficiente para demostrar la existencia de un código diferente de orden 5 para las secuencias no codificadoras.
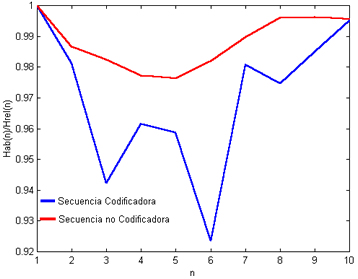
Figura 2. Entropía de Shannon normalizada vs. Orden de codificación en secuencias codificadoras y no codificadoras. Véase la preferencia por los órdenes 3 y 6 en las secuencias codificadoras.
La preferencia por un determinado orden no es tan clara para las secuencias no codificadoras; de hecho, algunas de estas secuencias mostraron ligera preferencia por los órdenes 4 y 6. Estos resultados, aunque preliminares, no descartan la existencia de algún tipo de 'seudo-código' en estas regiones, sin embargo para ello se requieren herramientas más sofisticadas. Actualmente esto esta siendo objeto de investigación por parte de nuestro grupo.
Es posible encontrar evidencias de estructura en secuencias genéticas relativamente cortas mediante el uso de la medida de complejidad de Lempel-Ziv.
En secuencias genéticas no codificadoras parece existir una ligera preferencia por órdenes de codificación diferentes del código de tripletes, sin embargo, no se demuestra la existencia de ningún otro 'código genético'.
Estas investigaciones se realizan bajo el auspicio del Centro de Cibernética Aplicada a la Medicina, La Habana.

BIBLIOGRAFÍA:
1. Clark AG .The search for meaning in noncoding DNA. Genome Research 2001; 11: 1319-1320
2. W Li . Int. J. Bifurcation Chaos 1992; 2:137.
3. Forsdyke DR . Symmetry observations in long nucleotide sequences. Bioinformatics 2002; 18: 215-217.
4. Shannon CE. A Mathematical Theory of Communication. The Bell System Technical Journal. 1948; 27: 379-423, 623-656.
5. Lempel A, Ziv J. On the complexity of finite sequences. IEEE Transaction on Information Theory. 1976; IT-22(1): 75-81.
6. http://biobases.ibch.poznan.pl/ncRNA/
7. Crutchfield JP, Young K. Inferring Statistical Complexity. Phys. Rev. Lett. 1989. 63:105.
8. Gell-Man M, Lloyd S. What is complexity. Complexity 1995.1(1):5.