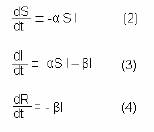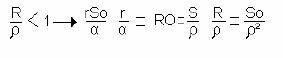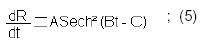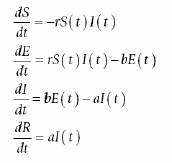Título: Modelo “SIR” para epidemias: Persistencia en el tiempo y nuevos retos en la era de la Informática y las pandemias. Autores: Karell R. Vázquez Argote. Instituto Nacional de Higiene, Epidemiología y Microbiología. INHEM. Lic. en enfermería. Residente de la especialidad de bioestadística segundo año. Instituto Nacional de Higiene, Epidemiología y Microbiología (INHEM). Infanta 1158 e/ Llinás y Clavel. Centro Habana. Calzada de infanta / manglar y Sto. Tomas. Teléfono: 870553 karell@inhem.sld.cu Maicel E. Monzón Pérez. Residente de Bioestadística. Máster en Informática en Salud. Instituto Nacional de Higiene, Epidemiología y Microbiología. INHEM. Infanta 1158 e/ Llinás y Clavel. Centro Habana. Teléfono: 8705531 Centro de Cibernética Aplicada a la Medicina. CECAM maicel@cecam.sld.cu maicel1978@yahoo.es José L. Hernández Cáceres. Doctor en Ciencias de la Salud. Profesor titular. Centro de Cibernética Aplicada a la Medicina. CECAM Dirección: Calle 146 #2511 Esq. 31 Playa, Cubanacan, Ciudad de La Habana, Cuba. CP: 11600 Telef. (537) 271-1354 cacerjlh@cecam.sld.cu Indice general Resumen. Introducción. Conclusión. Bibliografía. Resumen Los orígenes de la modelación moderna de epidemias datan desde 1927, con la propuesta de Kendrick y McCormick del modelo SIR (Susceptible, Infectado y Removido). Este enfoque ha impactado positivamente en el área de modelación y control de epidemias. En este trabajo se estudia el modelo SIR, así como algunas de sus modificaciones y se implementa un método para la solución numérica del sistema de ecuaciones diferenciales asociadas al modelo. No todo modelo logra impactar en la comunidad científica, y esclarecer las razones que hace posible que algunos sí lo consigan, reviste cierta importancia. Consideramos que la relevancia del modelo SIR se manifiesta desde diferentes ángulos, entre los que se destacan su simplicidad, su valor didáctico, su aplicabilidad a datos reales, su extensibilidad para el estudio de epidemias con mecanismos más complejos. Nuestro trabajo enfatiza en cada uno de estos aspectos y aborda nuevas interrogantes que impone la realidad de las epidemias de nuestro tiempo al ejercicio de su modelación. En particular, proponemos un nuevo enfoque para la estimación de los parámetros del modelo a partir de datos reales. Asimismo, se obtuvieron soluciones numéricas para un modelo de epidemias asociadas a vectores y se discute la eficacia de diferentes estrategias para su erradicación. En nuestra opinión, lograr romper las barreras que alejan la modelación matemática de los proveedores de salud pudiera revertirse en tomas de decisiones más justas y en la aprehensión de una cultura imprescindible en la era informática. Abstract The origins of modern research on epidemics date back to 1927, with Kendrick’s and McCormick’s “SIR” (Susceptible, Infected and Removed) model, whose impact in both modeling and epidemic’s control is outstanding. The present paper studied the dynamics of the SIR model and some of its modifications. A numeric solution method is introduced for solving differential equation system associated to the SIR model. Not every model is capable of being accepted by the scientific community, and to clarify the reasons why in certain cases it has been possible may be relevant. SIR model’s relevance can be regarded from different viewpoints, such as its simplicity, its applicability to the study of r real data, the possibility to extend it into epidemics with more complex mechanisms, as well as its didactic value. Our work emphasizes each of them, and approaches some of the challenges imposed to epidemics modelling in our time. In particular we propose a new approach for parameter estimation from real epidemic data. In this study we obtained numeric solutions for models of vector related epidemics and discuss the efficacy of different eradication strategies. In opinion, to break the barriers separating mathematic modelling from health providers must be beneficial for decision making, as well as for acquiring a needed culture at the age of informatics.   Introducción A partir del año 1950 la modelación matemática ha sido utilizada en la promoción efectiva de acciones de salud. Los orígenes de la modelación de epidemias, sin embargo, cuenta con una historia más larga. Hace 80 años Kendrick y McCormick propusieron el más importante de los modelos matemáticos para epidemias 1. Aunque no se trate de un olvido total de ese trabajo durante sus primeros 50 años (ver por ejemplo 2, 3), todo indica que su amplia difusión comenzó a partir de 1979 con el desarrollo de nuevas herramientas computacionales 4-9. Muchas de las barreras que impedían que modelos de este tipo fuesen del dominio de la comunidad médica se están derrumbando. Este modelo, conocido en la literatura como “SIR” (por sus siglas; Susceptible, Infectado y Removido) ha impactado positivamente en el área de modelación y control de epidemias. En nuestra opinión, su relevancia se manifiesta desde diferentes ángulos, entre los que se destaca: 1. Su simplicidad. La cual se hace palpable en la sencillez de su estructura pues solo cuenta con tres eslabones en su cadena. Esto permite una relativamente fácil obtención de las ecuaciones que definen el sistema. 2. Su valor didáctico. Diferentes aspectos comunes a toda epidemia, como su carácter explosivo, su naturaleza del tipo todo o nada, etc., pueden ilustrarse a partir del tratamiento de este modelo. 3. Su aplicabilidad a datos reales. En la medida que un modelo refleja la realidad, su utilidad es mayor y mayor es la certeza de que lo que se obtiene en el terreno de la modelación debe manifestarse en el curso de una epidemia. 4. Su extensibilidad para el estudio de epidemias con mecanismos más complejos. 5. La posibilidad de estimar sus parámetros. 6. Nuevas aplicaciones prácticas basadas en el modelo. El presente es un intento de valorar las virtudes del modelo SIR desde estos diferentes ángulos. En nuestra opinión, lograr romper las barreras que alejan la modelación matemática de los proveedores de salud pudiera revertirse en tomas de decisiones más justas y en la aprehensión de una cultura imprescindible en la era informática. 1. Breve descripción del modelo. Según el modelo SIR, un individuo susceptible (S) en contacto con un infestado (I), tiene cierta probabilidad de transitar él mismo a la condición de infestado. Por otra parte, la capacidad de infestar susceptibles no se mantiene siempre, sino que desaparece al cabo de cierto tiempo. Ese fenómeno de "clarificación" (remoción R=”removal”) puede ocurrir por diferentes mecanismos tales como curso natural de la enfermedad con inmunidad adquirida, muerte (común en epidemias como Ebola, SARS), o cuarentena. 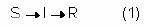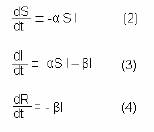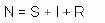Este modelo toma su nombre (SIR) del esquema que lo representa: Este esquema encuentra su representación matemática en el siguiente sistema dinámico: S se asume que la población es constante, entonces: Y bastará resolver las ecuaciones (2) y (3) para obtener la solución completa del sistema. En este sentido, la sencillez de este modelo incluye no solamente la sencillez del esquema matemático, sino también la sencillez y la plausibilidad de las ideas que lo sustentan. Hasta una persona sin preparación especial sabe que las enfermedades contagiosas se “pegan” y que al cabo de cierto tiempo la enfermedad “pasa” y casi nunca afectará de nuevo al mismo individuo. En modelación matemática, siempre habrá un compromiso entre hacer el modelo lo suficientemente sencillo como para que sea tratable matemáticamente y, por otra parte, hacerlo lo suficientemente abarcador como para que refleje los elementos esenciales de un fenómeno. Hasta las personas poco conocedoras saben que no todas las enfermedades contagiosas siguen ese esquema, pero lo sorprendente de este modelo es la gran cantidad de propiedades de una epidemia que pueden explicarse a partir del tratamiento matemático del modelo SIR. 2. Interpretación de las epidemias a partir del modelo. La solución del sistema (2-3) se obtiene al definir para cada momento de tiempo el valor de las variables I (t) y S (t). Aun cuando se trata de un modelo “simple”, no es posible obtener una solución analítica del mismo. Incluso para obtener soluciones analíticas bajo condiciones donde el problema matemático se simplifica considerablemente, se requiere ”...some elementary but tedious algebra...” (4). Sin embargo, es posible también extraer información importante acerca de una epidemia a partir de algunos cálculos bastante simples. 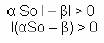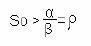Así, de la ecuación (3), se tiene que para que se desencadene una epidemia el número de infectados debe aumentar en su etapa inicial, por lo que: De donde: (A la magnitud se le conoce como tasa de eliminación relativa “relative removal rate”). Esto significa que la epidemia es un fenómeno umbral. Si en una comunidad dada, se cumple que el número de susceptibles es mayor que S0, en ese caso ocurra una epidemia. Desde el punto de vista práctico, este resultado muestra que disminuyendo la población de susceptibles (por ejemplo mediante la vacunación) es posible impedir el desencadenamiento de una epidemia. Este resultado teórico nos muestra que la vacunación selectiva cuando no es posible extenderla a toda la comunidad no es una opción inviable, pues el número de susceptibles no tiene necesariamente que ser igual cero. A diferencia de la solución analítica, obtener una solución numérica para un sistema de dos ecuaciones es relativamente fácil (20 segundos de cálculo en una Pentium II) en la figura #1 mostramos una simulación de una epidemia real obtenida a partir de una solución numérica del sistema. En ese sentido, el modelo SIR es un excelente apoyo para la comprensión de los mecanismos de una epidemia y las posibles vías para su control. 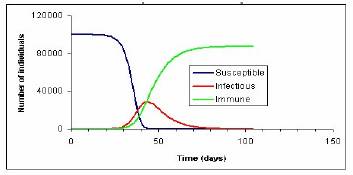Figura #1. Ver texto. 3. Aplicación a datos reales. Es evidente que ninguna epidemia real ocurre según un escenario tan simple. La etiología de los posibles vectores, factores climáticos, la estructura etárea de la población, diferentes fases del curso de la enfermedad, etc., pueden modular el desarrollo de una epidemia. Lo que resulta sorprendente es que un modelo tan simple sea capaz de corresponderse con un gran número de situaciones reales 4, 8. 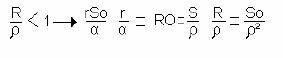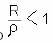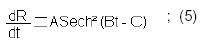Los propios autores del modelo SIR encontraron que bajo ciertas condiciones: Donde el número (lo que se corresponde a una epidemia “pequeña”) es posible obtener una solución analítica para la incidencia de “removidos” del sistema Curiosamente, esta aproximación es buena incluso para el caso de epidemias que no pueden considerarse como pequeñas. En particular, nuestro ajuste a una curva de un brote en una escuela interna donde la mayoría de los individuos se infestó (5), obtuvimos que el 95% de la varianza se explica si se aproximan los datos observados a una función del tipo (5). Lo mismo parece ser válido para el caso de algunas epidemias que no siguen el modelo SIR, como el caso del dengue, donde la infestación del vector y su interacción con el humano hacen más complejo el modelo. De esa manera, la aproximación con la secante hiperbólica parece ser buena para reproducir el curso temporal de la epidemia y también para obtener estimados aproximados sobre los parámetros del modelo. Al aplicar este modelo para ajustar datos reales obtuvimos que en un gran número de situaciones concretas los datos se describan satisfactoriamente en este modelo. De esta forma el modelo SIR permite obtener buenas aproximaciones a datos reales de epidemias. 4. Modelación de epidemias con mecanismos más complejos. En la literatura es posible encontrar ejemplos de modelos de epidemias donde se trata de caracterizar uno u otro tipo de mecanismo de infestación. Así, por ejemplo, en el modelo SEIR se diferencian susceptibles y latentes, mientras que las tasas de natalidad y mortalidad se incorporan al modelo. 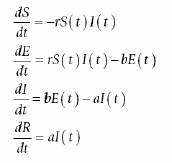En ese caso el sistema dinámico que corresponde a un modelo SEIR es: En la literatura se abordan con frecuencia modelos de diferentes grados de complejidad, lo que se resume en la figura #2. 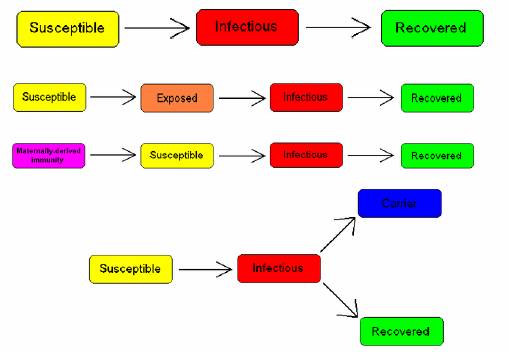Figura #2. Diferentes esquemas para modelos de epidemias. Modelos específicos, como el del dengue 10, representado en la figura #3 se han elaborado para diferentes enfermedades. 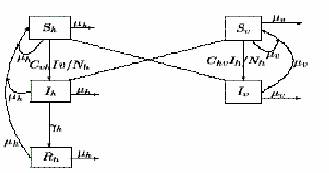Figura #3. Esquema para la epidemia de dengue. Modificado a partir de [10] Como se aprecia la gran diversidad de modelos tiene en común lo siguiente: • Todos preservan en su “esqueleto” el modelo SIR. • El planteo del modelo matemático se obtiene siguiendo la misma lógica utilizada en la implementación del modelo SIR. Cuando los modelos adquieren cierta complejidad, sin embargo, se hace difícil por una parte, obtener los parámetros a partir de los datos y, por otra parte, el tratamiento matemático se hace más difícil. Posiblemente esto permite explicar por qué los modelos particularmente complejos se utilizan fundamentalmente para simular y no tanto para estimar. En el otro extremo de la modelación aparecen los modelos conducidos por datos (“data-driven models”) donde la dinámica subyacente se obtiene partir de un modelo autorregresivo no lineal de toda la serie temporal 8, 12. Estos modelos son útiles para el caso cuando la enfermedad se hace endémica. La combinación de un enfoque basado en datos con una modelación mecanicista potenciaría notablemente los estadios de epidemias. En particular, nuestro grupo, utilizando técnicas de identificación no lineal, ha encontrado evidencias de bifurcaciones en la dinámica no lineal del sarampión en la época anterior a la vacuna 11, lo que se corresponde con las predicciones planteadas por otros autores para un modelo SEIR. 5. Estimación de parámetros. En el marco de un modelo SIR es relativamente fácil obtener el comportamiento del sistema dado un conjunto de parámetros. La tarea inversa, es decir, determinar los parámetros del modelo a partir de datos observables requiere de una especial experticia. Dadas las actuales posibilidades de los métodos de cómputo, es posible implementar un método que ajuste la solución dados unos parámetros a un grupo de datos reales. Esa opción no aparece implícita en ninguno de los paquetes estadístico conocidos ni en los sistemas de solución de ecuaciones diferenciales. No obstante, su implementación es fácil de lograrse. Mediante el ajuste de datos a la expresión de secante hiperbólica propuesta por Kendrick y McCormick, es posible estimar algunos parámetros importantes de la epidemia. La combinación de métodos numéricos con técnicas de optimización permitiría estimar el conjunto de parámetros del sistema dinámico que mejor representan los datos. Una tarea de ese tipo es alcanzable, dado el actual desarrollo de las técnicas numéricas 8, 13. 6. Nuevas aplicaciones prácticas basadas en el modelo. En esta sección se describe una metodología propuesta por nuestro grupo para la predicción del curso de una epidemia. Uno de los resultados más interesantes del tratamiento matemático del modelo SIR es la predicción de que bajo ciertas condiciones plausiblemente aceptables es posible predecir la frecuencia de remoción (removal rate dR/dt) mediante la expresión: dR /dt=A*sech2(B*t-C) Donde A, B, C son constantes y t es el tiempo. Entre las características más notables de esta función se destacan su simetría, y el hecho de que el valor máximo se obtiene cuando el argumento de la cotangente hiperbólica se iguala a cero. Eso ocurre cuando T pico=C/B. En condiciones de adecuado monitoreo de la epidemia dR/dt equivale a la incidencia de casos, pues en esas condiciones el paciente se hospitaliza o se somete a cuarentena. En particular, Murray trata el ejemplo de la epidemia de peste en Bombay en 1905-1906. La figura #4 reproduce los datos registrados semanalmente de la figura 19.2 del texto de Murray 4. 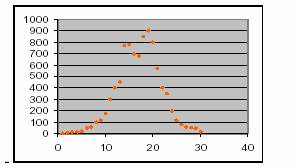Fig. 6. Datos de una epidemia de peste en Bombay 4. Según Murray, los siguientes parámetros se ajustan adecuadamente a los datos: A=890 B=0.2 C=3.4 Como se aprecia, el valor máximo se corresponde a C/B=3.4/0.2=18, lo que parece ser una aproximación plausible. Al estimar los parámetros mediante un algoritmo de optimización, por el método de Gauss Newton (Grave et al, 1991), obtuvimos los siguientes valores para el caso cuando se incluyeron los datos de las 30 semanas: A=865 (3%) B=0.2 (0%) C=3.2 (6%) Como se observa, existe una gran concordancia entre las dos estimaciones. Los resultados, como es de esperar, dependen fuertemente del número de puntos que se usen para la estimación. Esos resultados se han reflejado en la Tabla I. 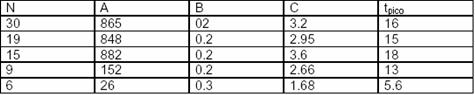Tabla I. Dependencia de los parámetros del modelo respecto al número de puntos que se incluyan para la estimación. Como se aprecia de la tabla I con la mitad de los puntos de la onda es posible obtener buenos estimados de los parámetros. Cuando se toma el 25% de los puntos iniciales de la onda, se aprecia que el valor del pico de incidencia está muy distorsionado, cayendo hasta menos del 4 por ciento de su valor real. No obstante, en esas condiciones se obtienen buenos estimados de los componentes que caracterizan el curso temporal de la epidemia. Utilizando solamente 6 puntos la correspondencia con la realidad se distorsiona notablemente. Más adelante proponemos un método que permite obtener estimados plausibles de los parámetros de la epidemia utilizando un número pequeño de puntos de la fase inicial. Por definición, la cosecante hiperbólica es el inverso del coseno hiperbólico, por lo que la expresión (1) puede representarse como: dR/dt=A/(cosh2(B*t-C)) (2) Para comodidad del análisis ulterior, representamos dR/dT=Y, representando con Y la incidencia de la enfermedad. Y(t)=A/(cosh2(B*t-C)) (3) La aproximación del coseno hiperbólico con serie de Taylor indica que Cosh(x)=1+x2/2! + X4/4! +… La expresión recíproca de (3) nos sugiere (1/Y(t))= (cosh (B*t-C))2 / A (1/Y(t))1/2= (cosh (B*t-C)) / A1/2 =~ A-1/2 * (1+(1/2)* (B*t-C)2+(1/24)*(B*t-C)4) (4) A partir de (4) se hacen las siguientes aproximaciones. Por cuanto C>1, B<0, se justifica, para valores pequeños de t, eliminar el 1 en el polinomio de la expresión (4), por lo que (1/Y(t))1/2 =~ A-1/2 *(B*t-C)2 *((1/2) +(1/24)*(B*t-C)2) (5) Para valores pequeños de t debe cumplirse t<0.5C/B, mientras que C<24, para la mayoría de las situaciones reales. Por lo que la expresión entre paréntesis debe ser mayor de 0.5, pero no mayor de 1, por lo que ese miembro puede tomarse como próximo a la unidad, de modo que ((1/Y (t))1/4)=~ K*(B*t-C) (6). De esta manera, para valores iniciales de la epidemia debe existir una relación aproximadamente lineal entre la raíz cuarta del recíproco de los datos de incidencia y el tiempo. Debe cumplirse además que la relación entre los dos coeficientes de la ecuación deba ofrecer un estimado del momento pico de la epidemia. Esta relación lineal no debe extenderse hasta el momento del pico, pero la función lineal evaluada en algún punto anterior al máximo debe brindar un buen estimado del valor máximo de incidencia. Comportamiento de datos reales. 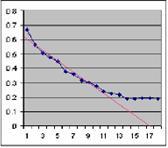Figura 7. Ilustración del método. Datos de la figura 6. Como se aprecia de la figura 7, donde se transformaron los datos de la figura 6, los primeros puntos se aproximan a una función lineal, con pendiente aproximadamente igual a 0.038 e intercepto igual a 0.65. La relación de los parámetros predice un valor máximo de 0.65/0.038=17 semanas, cercano al valor obtenido con todos los datos, mediante el método clásico (16 semanas). El valor máximo (mínimo en esta gráfica de recíprocos se obtiene al extrapolar la recta a un valor de 12 semanas). Lo que significa el 75% del momento pico estimado. Aplicando este método se obtiene un valor para el máximo de la epidemia de 625 casos por semana, lo que se acerca al 72% del estimado original. Como se aprecia de la gráfica, usando los primeros días de la epidemia es posible obtener la recta a partir de la cual se predicen las características de la misma. Datos de dengue. Epidemia de Santiago de Cuba (1997) 14. Como se observa en la figura 8, el método fue capaz de predecir el momento del pico de esta epidemia. Se obtuvo asimismo una predicción satisfactoria para el número de casos en el pico. 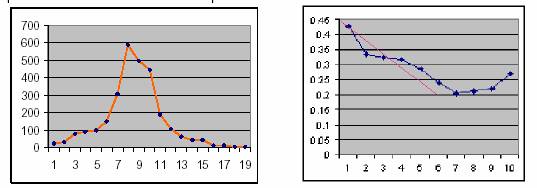Figura 8. Datos de dengue en Santiago de Cuba 14 Como se aprecia, el método puede ser útil para evaluar la severidad de una epidemia que está en marcha. Conclusiones El modelo SIR es plausible y simple tanto en las ideas de su mecanismo básico como en su formulación matemática. Propiedades importantes de las epidemias, como su carácter umbral, la manera explosiva en que ascienden, etc. pueden ser explicadas a partir del modelo SIR. El modelo es capaz de reproducir datos de disímiles epidemias, en particular, la solución simplificada con una función secante hiperbólica se ajusta a conjuntos de datos reales. Mediante las adaptaciones correspondientes, el modelo puede extenderse al caso de epidemias con mecanismos más complejos, como ocurre con epidemias inducidas por vectores. Mediante técnicas de aproximación de funciones es posible estimar los parámetros que caracterizan una epidemia. La metodología propuesta, que se basa en una extensión del modelo SIR, permite predecir el curso de una epidemia a partir de los datos iniciales. Bibliografía Kermack, W. O., McKendrick, A. G. Contributions to the mathematical theory of epidemics. Proc. Royal Soc. A, 115, 700-721 (1927). Defares J G, Sneddon I N. The mathematics of Biology and Medicine. Editora Revolucionaria. La Habana, 1970. Bailey NTJ: The Mathematical Theory of Infectious Diseases and its Applications. 2nd Edition. Griffin, London. 1975. Murray J D. Mathemativcal Biology. Springer Verlag. Berlin Heidelberg. 1990. Ellner S P, Bailey B A, Bobashev G V, Gallant A R, Grenfell B T, Nychka D W. Noise and Nonlinearity in Measles Epidemics: Combining Mechanistic and Statistical Approaches to Population Modeling. American Naturalist, Vol. 151, No. 5 (May, 1998), pp. 425-440. O. Diekmann and J. A. P. Heesterbeek. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation. Wiley, 2000. H. W. Hethcote. The mathematics of infectious diseases. SIAM Review, 42(4):599–653, 2000. Bjørnstad ON, Finkenstäd, B, and Grenfell BT. (2002) Dynamics of Measles Epidemics: Estimating Scaling of Transmission Rates using a Time Series SIR Model. Ecological Monographs 72 169-184. Wai-Yuan Tan, Hulin Wu DETERMINISTIC AND STOCHASTIC MODELS OF AIDS EPIDEMICS AND HIV INFECTIONS WITH INTERVENTION. World Scientific. 2005. Derouich M, Boutayeband A, Twizell EH. A model of dengue fever. BioMedical Engineering OnLine 2003, 2:4. Hernández Cáceres JL, Hernández Martínez L, Pérez Monzón M, and García Domínguez L. Nonlinear properties of measles epidemic data assessed with a Kernel Nonparametric Identification approach. Elect J. Biomedicine, No1, 2006. Stark J and Hardy K. Chaos. Useful at last? Science 301, 1192-1193, 2003. John J. Potterat, Helen Zimmerman-Rogers, Stephen Q. Muth, Richard B. Rothenberg, David L. Green, Jerry E. Taylor, Mandy S. Bonney and Helen A. White. Chiamydia Transmission: Concurrency, Reproduction Number, and the Epidemic Trajectory American Journal of Epidemiology Vol. 150, 1999, No. 12: 1331-1339. Kouri G, Guzmán MG, Valdés L, Carbonell I, Rosario D, Vázquez S, S, Laferte, J, Delgado J, Cabrera MV . Reemergence of dengue in Cuba: a 1997 epidemic in Santiago de Cuba. Emerg Infect Dis 1998;4:89–92.