Autor:
Héctor
Simón Vargas Martínez
Ingeniero en Computación. Universidad Popular Autónoma
del estado de Puebla, Méjico.
E-mail: hvargas@divtec.pue.upaep.mx
RESUMEN
Basándose
en los trabajos de Khalimsky y Kovalevsky, los cuales propusieron
que una imagen digital está asociada a un espacio topológico,
se propone en el presente artículo un nuevo algoritmo basado
en estos conceptos de topología general y enmarcado en
el modelo difuso. Se hace un análisis de los resultados
que arroja el algoritmo sobre las imágenes, como el grado
de compactificación de los objetos en cada clase, así
como la separabilidad de las clases; también se analiza
la complejidad en tiempo y espacio del algoritmo. Se presenta
como parte de las conclusiones la opinión de un experto
para evaluar los resultados de la segmentación y se explica
en las perspectivas la importancia del concepto de segmentación
en el proceso de diagnóstico.
ABSTRACT
Based on Khalimsky
and Kovalevsky works, which proposed that a digital image is associated
to a topological space, it is proposed in this work a new algorithm
based on the general topology concepts and within the diffused
model . An analysis is made about the results of the algorithm
about the images such as the compactification degree of the objects
in each class and the separability of the classes; it is also
analyzed the time- and space complexity of the algorithm. We present
as part of the conclusions the opinion of an expertise to evaluate
the results of the segmentation. It is also explained the importance
of the segmentation concept in the diagnosis process.
INTRODUCCIÓN
La clasificación
de tejidos de imágenes de resonancia magnética (RM)
(2) y tomografía computarizada (TC) (1)
es un proceso en el cual los elementos de imagen que representan
el mismo tipo de tejido son agrupados en un solo conjunto y son
referenciados en una misma clase (los elementos de imagen son:
de dos dimensiones, llamados píxeles, o de tres dimensiones,
llamados voxels). Los diferentes grupos de voxels clasificados
son etiquetados por números enteros diferentes para desplegarlos
en la computadora. El proceso de asignar de forma apropiada etiquetas
de clases a todos los voxels en el arreglo de voxels es llamado
segmentación (3). La segmentación
identifica, por las etiquetas, regiones de diferentes tipos de
tejidos, o separa regiones de un mismo tipo de tejido en el arreglo
de voxels que aparecen uniforme al observador.
Existe una
diversidad de equipos, desde los austeros hasta los más
sofisticados, que integran en su sistema varias etapas significativas,
las cuales tienen la finalidad de ser una herramienta más
para el especialista en la obtención del diagnóstico.
Sin embargo, una de las etapas de cualquier sistema requiere especial
atención, la segmentación de imagen. Aunque esta
ya ha sido analizada y resuelta en diferentes modelos (4)
se siguen haciendo nuevas propuestas o haciendo mejoras de los
algoritmos existentes. Así, el presente artículo
propone un nuevo algoritmo basado en conceptos de topología
general en el modelo difuso.
La sección
2 presenta la formalización matemática de la segmentación
de imagen, para después continuar con el algoritmo topológico,
en la sección 3. En la sección 4 se dan las conclusiones
y perspectivas.
DESARROLLO:
Segmentación
de la Imagen
Una de las
principales etapas del análisis de imagen y del reconocimiento
es la segmentación de la imagen en regiones y el cómputo
de varias propiedades de las relaciones entre estas regiones.
Sin embargo, las regiones no siempre son duramente definidas;
a veces es más apropiado mirarlas como subconjuntos difusos
de la imagen (5).
En esencia,
la segmentación consiste en hallar la estructura interna
del conjunto de descripciones de los objetos (píxeles)
en el espacio de representación (imagen). Esta estructura
interna evidentemente depende, en una primera instancia, de la
selección de los píxeles y de la forma en que éstos
se comparan, es decir, del concepto de similaridad que se utilice
y de la forma en que este se emplee (6).
Existen cuatro
modelos para etiquetar clases o segmentarlas: duro, difuso, probabilístico
y posibilístico. A continuación se dan algunas definiciones
sobre estos modelos.
Definición
1. Sea c un entero el cual denota el número de
clases, 1 £ c £ n, y definimos tres conjuntos de vectores-etiquetas
en Rc como sigue:
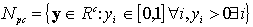
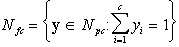
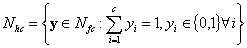
Nhc
es la base canónica de Rc; Nfc representa una pieza de un hiperplano, es su envolvente convexa;
y Npc es un hipercubo en Rc, excluyendo el origen. El i-ésimo vértice de Nhc es
ei
= (0, 0, . . . , 1, . . . , 0)T
es la etiqueta
dura para la clase i, 1£ i £ c. El vector y = (0.1,
0.6, 0.3) T es un vector-etiqueta forzado; sus entradas están
entre 0 y 1, y su suma es 1. Si y es una etiqueta para algún
xÎRp generado por el modelo fuzzy-c-means [7], llamamos
a y una etiqueta difusa para x. Si y viene de un método
tal como la estimación de probabilidad máxima, y
será una etiqueta probabilística. Los vectores tal
como z = (0.7, 0.2, 0.7) en Npc = [0, 1]-{0}son llamados vectores-etiquetas
posibilísticos.
Cuando X no
está etiquetado, la asignación de vectores-etiquetas
a sus elementos es precisamente el proceso de agrupamiento o segmentación
(o aprendizaje no supervisado). Si las etiquetas son duras, esperamos
que ellos identifiquen a los c subgrupos naturales (clases de
tejidos) de X.
Definición
2. La c-partición de X son conjuntos de (c´n)
valores {uik} que son arreglados en una matriz de (c´n),
U = [U1, . . . , Uk, . . . , Un] = [ uik ], donde Uk denota la
k-ésima columna de U:
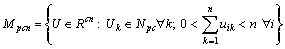
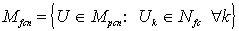
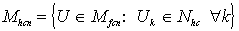
las ecuaciones
definen, respectivamente, los conjuntos de las c-particiones de
X como posibilístico, difuso (o probabilístico)
y duro. Cada columna de U en Mpcn (Mfcn, Mhcn)
es un vector-etiqueta de Npc (Nfc, Nhc). Note que Mhcn Ì
Mfcn Ì Mpcn. Si U es difuso, uik es la
pertenencia de xk en el i-ésimo grupo difuso de X.
El agrupamiento
difuso, incluyendo trabajos en procesamiento de imágenes
difusas y segmentación, es discutido en Bezdek y Pal [20].
Definición
3. Los algoritmos de agrupamiento son funciones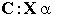 
Rc,
donde Rc
es el rango de C. Cuando la salida de C es justamente una partición,
entonces Rc = Mpcn.
Recuerde que
algunos algoritmos de agrupamiento producen particiones buenas
en el modelo difuso. La asignación a clases para cada píxel
es el objetivo usual en la segmentación de imagen, sin
embargo, para el modelo difuso las etiquetas en Npc
son a menudo transformados en etiquetas duras.
Definición
4. Las etiquetas no duras y son usualmente convertidas
a etiquetas duras usando la función de conversión:
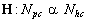
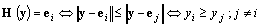
donde 
es la norma Euclidiana, 
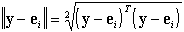en
Rc. H encuentra la etiqueta dura para
el vector ei en el conjunto cerrado Nhc
para y. Alternativamente, H
encuentra la coordenada máxima de y, y
lo asigna a la correspondiente etiqueta dura del objeto z
que etiqueta y. Note que, la razón para
usar H depende en gran medida del algoritmo que
produce y.
Resumiendo
pudiéramos decir que en un problema de segmentación
(o clasificación sin aprendizaje) los tres elementos
esenciales son: el espacio de representación de los
objetos, la medida de similaridad (función de semejanza,
no necesariamente una distancia) y el criterio de agrupamiento,
es decir, la manera en que será utilizada la similaridad
para la solución del problema planteado.
Los algoritmos
de agrupamiento pueden ser categorizados, tanto por una base axiomática:
determinístico, estadístico, difuso
y posibilístico (7), como por
el criterio agrupacional; existen tres tipos de criterios para
cada clase axiomática: función objetivo, teoría
de grafos, jerárquicos.
3.
ALGORITMO TOPOLÓGICO
Khalimsky,
(1977,1986), y más recientemente Kovalevsky, (1988), propusieron
que una imagen digital está asociada a un espacio topológico
(8). Entonces, en lugar de tener que definir
nociones de topología para el concepto de grafos (tales
como conectividad) para imágenes digitales, las nociones
de topología general pueden ser usadas más directamente.
En el procesamiento de imágenes el estudio de las propiedades
topológicas de una imagen se ha desarrollado a través
de la teoría de grafos (más comúnmente conocidos
como relaciones 4-,8-, .. relaciones de adyacencia) (5),
sin embargo, la topología general brinda importantes conceptos
que se pueden utilizar en el análisis de imágenes,
como es el objetivo de este artículo, proponer un nuevo
criterio agrupacional para la segmentación de imágenes.
Por lo tanto, el artículo presenta una nueva propuesta
que consiste en un algoritmo de clasificación sin aprendizaje,
el cual está dado a partir de la definición de un
criterio agrupacional, que a la vez está definido sobre
conceptos topológicos. (10,11)
Sobre la idea
de estos conceptos y los que de alguna manera están implicados,
se presenta el siguiente criterio agrupacional, el cual nos dice
cuándo un elemento pertenecerá a un subconjunto
de la imagen o cuándo este elemento generará un
nuevo grupo. La siguiente definición nos permite construir
un cubrimiento de X a partir de X.
Definición
6. Sea X el conjunto imagen y sea S
Í P(X) se define j: S´X
® [0, 1], tal que
j( A, x) =
d(d(A), x)
con d(A) =
supy,z ÎA{d(y,z)}
Decimos entonces
que j es una función que nos da la relación de semejanza
del conjunto A Î S con x Î X, a partir
precisamente de considerar el diámetro del conjunto A y
la relación de su diámetro con todos sus elementos.
Esta función depende de la aplicación que se esté
considerando.
Definición
7. Dados e , d Î [0, 1] fijos y S Í P(X).
Sea X un conjunto imagen y sea A Î S ,
se dice que un elemento x Î X pertenece
a A si se cumple que
Be(x) Ç
A\{x} ¹ Æ Ù j( A\{x}, x) < d
en otras palabras,
S es un cubrimiento de X.
La definición
nos plantea cuándo un elemento pertenece a un subgrupo
del potencial de X, el cual constituye precisamente una segmentación
de la imagen. La construcción de este cubrimiento S (como
sucesión) está determinada por las propiedades que
la definen, esto es, un elemento de la imagen pertenecerá
a un elemento de S si existe una bola con centro en el punto y
un radio dado tal que intercepte al subconjunto y además
que dicho elemento esté relacionado con el subconjunto
que es elemento de S.
No estamos
pidiendo que los grupos sean disjuntos dos a dos, sino que se
permita también el solapamiento, además podemos
pensar en el concepto difuso para conocer cómo se comportan
las pertenencias de los elementos en los grupos con relación
a su vecindad local y a sus representantes.
El algoritmo
usa el criterio agrupacional definido anteriormente para generar
la segmentación de la imagen. El mismo inicia su búsqueda
etiquetando el primer píxel que encuentra en el principio
de la imagen (suponiendo un orden o una dirección), de
ahí parte para aglomerar a sus vecinos más semejantes
y computar j(A, y) simultáneamente en la formación
del grupo, o ir formando los demás grupos con la misma
idea.
Dados e y
d fijos. Se crea el primer conjunto A1 = {x} tal que x Î
X, con n = 1.
PASO
1: Mientras $ y Î X tal que
y Ï Ai "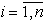 
hacer paso 2 y 3.
si no existe
y Î X ir al paso 4.
PASO
2: Para hacer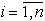 
Si N(y;
e)Ç Ai ¹ Æ Ù j( Ai, y) < d
entonces
I = I È {i}
PASO
3: Si I ¹ Æ entonces Ai = Ai È {y}
" i Î I.
de lo contrario
n = n+1
An = An
È {y}
PASO
4: Formados los grupos, se procede con el análisis
de la dirección que se presentó en la búsqueda
de la formación de la estructura de los mismos. Esto
es, hace una reubicación de los píxeles porque
éstostienen un cierto comportamiento por la dirección,
(con la misma idea del criterio agrupacional topológico).
En la búsqueda
de las estructuras vamos recordando los grupos formados y la información
que ellos proporcionan por el valor de j(A, y) y sus elementos,
además, como se va caminando en una dirección, el
resultado dependerá en alguna medida de la dirección
elegida, por tal razón, una vez terminada la búsqueda
de las estructuras de los grupos, antes de entrar al paso
4, como todos los píxeles están etiquetados,
entonces se puede despreciar la dirección y concentrarse
más en la relación que guardan los vecinos con su
vecindad local y global.
RESULTADOS
Los datos
de entrada del algoritmo topológico fueron las imágenes
presentadas en la figura 1, la primera de ellas
fue adquirida de la tomografía computarizada y la otra
de la resonancia magnética. Estas imágenes tienen
dimensiones de 256´256 píxeles, donde cada píxel
tiene un valor entre 0 y 5000. Cada objeto o elemento de la imagen
está representado por un píxel, el cual a su vez
está formado por cinco rasgos que fueron calculados dentro
del dominio espacial. Estos conjuntos de imágenes fueron
difusificados y por esto caen dentro de la definición
1, así como también el algoritmo topológico
genera un cubrimiento de la imagen que a su vez cuadra con la
definición 2, esto es, constituye
una c-partición. El resultado son nuevas imágenes
(figura 2), las cuales están coloreadas
con relación al agrupamiento creado por dicho algoritmo,
esto es, cada subgrupo está etiquetado con un color; el
orden de los intervalos presentados en cada imagen está
en relación con la paleta de colores que maneja la computadora.
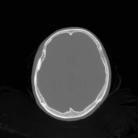
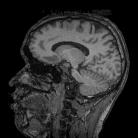
Figura
1: Imágenes adquiridas de la TC y RM respectivamente,
representan los datos de entrada para el algoritmo de segmentación
previa fuzificación.
En la figura
2, en la primera imagen izquierda, se crearon 9 grupos, los cuales
se dan en los siguientes intervalos: (2, 44), (42, 120), (105,
191), (156, 258), (222, 317), (281, 361), (325, 381), (403, 446)
y (513, 513). Mientras en la siguiente imagen (derecha), se crearon
10 grupos, los cuales se dan en los siguientes intervalos: (2,
284), (238, 642), (572, 1272), (970, 1654), (1234, 1910), (1650,
2206), (2092, 2474), (1692, 1708), (544, 870) y (1324, 1324).
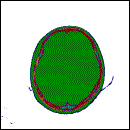
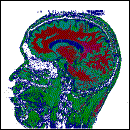
Figura
2.
Resultado del algoritmo de segmentación topológico.
Para obtener
la complejidad del algoritmo propuesto, se analizó el algoritmo
considerando que en un recorrido encuentra todos los subgrupos
de la imagen sin tomar en consideración si no son disjuntos,
después continúa con otro recorrido para corregir
la dirección en la creación de los grupos, por tanto,
la complejidad computacional en tiempo es lineal por un factor
de 7, esto es 7n. La complejidad en espacio depende del número
de grupos creados, pero como se presentó en todos los resultados,
como promedio tenemos 9 grupos por imagen, esto es, el tamaño
en memoria para mantener el resultado es 2´256´256´9
bytes. Se probó el algoritmo en una PC a 100 Mhz con 16
Mb de RAM, el algoritmo consumió, para una imagen, aproximadamente
5 segundos.
Ahora, para
obtener la separabilidad, primero se define la separación
de un agrupamiento difuso como la suma de las distancias de sus
centros de agrupamiento a los centros de los otros agrupamientos,
se trabajó con los índices de validación
propuestos en (15), los cuales encuentran la
mínima distancia entre los centros de los agrupamiento,
por lo cual, cuanto menor valor obtenga la función de validación,
indica una mejor partición de la imagen; en nuestro experimento
el valor obtenido es de 0.212. Mientras que la compactificación
es la suma de las desviaciones difusas de los objetos en el subgrupo
entre la suma de las cardinalidades difusas de los agrupamientos,
la cual para nuestro experimento también resultó
muy aceptable.
CONCLUSIONES
El propósito
de la clasificación y segmentación de tejidos en
imágenes médicas es cuantificar el tamaño
de diferentes tipos de tejidos, y poder desplegar, en la pantalla,
las estructuras de los mismos para, por ejemplo, facilitar la
cirugía y la terapia. Por esta razón, es muy importante
proponer nuevos algoritmos, como lo es el presente, para tratar
de encontrar estas estructuras de grupo.
En nuestro experimento se usaron tres conjuntos de datos de dominios
diferentes, los cuales revelaron la adopción de la mínima
distancia de separación para la validación de partición,
pudiendo ser útil cuando se busque un número óptimo
de agrupamientos, pero no cuando se comparan diferentes particiones
teniendo un número igual de agrupamientos.
Los algoritmos
de segmentación no requieren de entrenamiento de datos,
sin embargo, para un conjunto de datos, se proporcionan diferentes
algoritmos de segmentación para producir diferentes agrupamientos
de los objetos; en resumen, una partición generada por
un algoritmo de agrupamiento no siempre corresponde a la clase
fundamental.
El algoritmo
topológico genera un cubrimiento del conjunto, permitiendo
con esto el solapamiento de los subgrupos creados y obteniendo
de una manera natural la estructura difusa de los subgrupos creados.
También cabe mencionar que el algoritmo trabaja sin ningún
problema en la tercera dimensión, esto es, considerando
en su conjunto el arreglo de datos volumétricos, de esta
manera se obtienen mejores resultados.
REFERENCIAS
BIBLIOGRÁFICAS
1.
Henry J. Scuddder. “Introduction to Computer Aided Tomography”.
Proc. IEEE, vol. 66, pp. 628-637, June 1978.
2.
Waldo S. Hinshaw and Arnold H. Lent. “An Introduction to
NMR Imaging: From the Bloch Equation to the Imaging Equation”,
Proc. IEEE, vol. 71, pp. 338-350, March 1983.
3.
Zhengrong Liang. “Tissue Classification and Segmentation
of MR Images”, IEEE Engineering in Medicine and Biology,
March 1993.
4.
J. C. Bezdek and L.O. Hall, Matt Clark, Dmitri Goldgof and L.P.
Clarke, “Segmenting Medical Images with Fuzzy Models An
Update”, Fuzzy Information Engineering 1997.
5.
J. C. Bezdek, “Fuzzy Sets for Pattern Recognition”,
1986.
6.
J. R. Shulcloper, “Reconocimiento de Patrones”, notas
del autor.
7.
J. C. Bezdek and S. K. Pal, “Fuzzy Models for Pattern Recognition”,
Piscataway: IEEE Press, 1992.
8.
de Olivera, R.I. Kitney, “Texture Analysis for Discrimination
of Tissues in MRI Data”, Proceedings, Computers in Cardiology.
pp. 481-484. Piscataway:IEEE Press. 1992.
9.
Pattern Recognition and Analysis of the image.
10.
Robert L. Cannon, Jitendra V. Dave and James C. Bezdek, “Efficient
Implementation of the Fuzzy c-Means Clustering Algorithms”,
IEEE Trans. Pattern Analysis and Machine Intelligence, vol. PAMI-8,
no. 2, March 1986.
11.
Reed, Roscoe, Wachter, “Topology and Category Theory in
Computer Science”, Oxford Science Publications, 1991.
12.
Iribarren, “Topología de Espacios Métricos”,
Limusa 1987.
13.
A. R. Páramo, “Tópicos en Topología”,
Edición del Autor, 1995.
14.
Aho, Hopcroft, Ullman, “Data Structures and Algorithms”,
Addinson- Wesley Publishing Company, Reading Massachusetts, E.U.A.
1983.
15.
L. X. Xie and G. Beni, “A validity measure for fuzzy clustering”,
IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 13,
pp. 841-847, Aug. 1991.
