| |
Titulo: The Standard Genetic Code and its relation to mutational
pressure: Robustness and equilibrium criteria.
Autores:
José Luis Hernández Cáceres¹-², Rolando
Hong¹, Carlos Martínez Ortiz¹, Miguel Sautié
Castellanos¹, Kiria Valdés1 and Ramón Guevara
Erra².
¹Bioinformatics Section, Center for Cybernetics Applications
to Medicine, CECAM-ISCMH, Havana, Cuba.
²The Abdus Salam International Center for Theoretical Physics
(AS-ICTP), Trieste, Italy.
Índice
general
ABSTRACT.
Under the assumption of even point mutation pressure on the DNA
strand, rates for transitions from one amino acid into another were
assessed. Nearly 25% of all mutations were silent. About 48% of
the mutations from a given amino acid stream either into the same
amino acid or into an amino acid of the same class. These results
suggest a great stability of the Standard Genetic Code respect to
mutation load. Concepts from chemical equilibrium theory are applicable
into this case provided that mutation rate constants are given.
It was obtained that unequal synonymic codon usage may lead to changes
in the equilibrium concentrations. Data from real biological species
showed that several amino acids are close to the respective equilibrium
concentration. However in all the cases the concentration of leucine
nearly doubled its equilibrium concentration, whereas for the stop
command (Term) it was about 10 times lower. The overall distance
from equilibrium for a set of species suggests that eukaryotes are
closer to equilibrium than prokaryotes, and the HIV virus was closest
to equilibrium among 15 species. We obtained that contemporary species
are closer to the equilibrium than the Last Universal Common Ancestor
(LUCA) was. Similarly, non-preserved regions in proteins are closer
to equilibrium than the preserved ones. We suggest that this approach
can be useful for exploring some aspects of biological evolution
in the framework of Standard Genetic Code properties .
¹This paper was prepared during a working visit by JLHC to
the AS-ICTP, where he is a Senior Associate, and was approved as
a preprint under the number IC/2004/100 (www.ictp.it/
?pub_off)
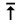
Introduction
Results from the theory of linear differential equations have boosted
many fields of natural sciences, from quantum mechanics to microbiology.
Particularly useful is that result stating that for a system of
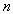 elements elements 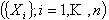 if
the linear rate of transition between elements if
the linear rate of transition between elements 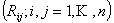 may
be defined, it is possible to determine the quantities (proportions,
concentrations) of each element after a long time of spontaneous
evolution may
be defined, it is possible to determine the quantities (proportions,
concentrations) of each element after a long time of spontaneous
evolution 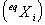 .
For computing these "equilibrium" concentrations, the
state of the system at any given moment is not needed to be known.
This result finds application in such areas as the mass action law
for chemical equilibrium. In this paper an attempt is made to apply
the same ideas to the transition between the codons corresponding
to amino acids in a codifying region of DNA. Since the bulk of naturally
occurring mutations are point mutations involving only one letter
change in the codon, the first version of our model will consider
this type of mutations only 1. As it is known,
given the Standard Genetic Code (SGC), a point mutation may lead
or not lead to a change in the amino acid codified by the unmutated
codon. Under certain plausible assumptions it is possible to mathematically
model the process. Not only amino acids are codified by the SGC,
and there is no especial rule for the transitions, thus we regard
the stop command (Term), codified by three codons, as a "virtual
amino acid". .
For computing these "equilibrium" concentrations, the
state of the system at any given moment is not needed to be known.
This result finds application in such areas as the mass action law
for chemical equilibrium. In this paper an attempt is made to apply
the same ideas to the transition between the codons corresponding
to amino acids in a codifying region of DNA. Since the bulk of naturally
occurring mutations are point mutations involving only one letter
change in the codon, the first version of our model will consider
this type of mutations only 1. As it is known,
given the Standard Genetic Code (SGC), a point mutation may lead
or not lead to a change in the amino acid codified by the unmutated
codon. Under certain plausible assumptions it is possible to mathematically
model the process. Not only amino acids are codified by the SGC,
and there is no especial rule for the transitions, thus we regard
the stop command (Term), codified by three codons, as a "virtual
amino acid".
Hopefully, this model can shed some light into certain aspects of
biological evolution using relatively simple ideas. Thus, for example,
the degree of closeness to equilibrium may provide information about
the pace at which evolution is proceeding. One may also try to predict
how this evolution will continue, or even how the amino acid composition
at the eve of evolution looked like.
On the other hand, most of the attempts to characterize the genetic
code consider it robustness with respect to mutations 1-4.
However, an absolutely robust code will leave no room for evolution
and biodiversity 4. Measures for the robustness
of the SGC have been proposed by others as a way to show its optimality
1-2, especially in the framework of trying to understand
how the genetic code appeared on Earth. The approach introduced
here may serve for evaluating both SGC's robustness, as well as
its evolution potential.
Method
Assumptions
of the model.
We assume the
following:
1. If an amino acid is codified by more than one codon, each synonymic
codon is used with the same frequency. In a coming section, the
case will be considered of the effects of unequal codon usage.
2. All point mutations occur with the same probability. It means
that the chance for a change from a basis k into another
basis l in the DNA is identical to any other base change.
3. Mutation probability remains the same all along the DNA strand.
No preferences for position in the codon are considered.
4. The stop command (Term) is formally regarded as an "amino
acid" since there is a probability in the space of codons for
any amino acid to become a stop command and vice-versa via
a point mutation.
5. The transition rate 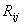 is
proportional to the number of point mutations leading from the ith
amino acid toward the jth one. is
proportional to the number of point mutations leading from the ith
amino acid toward the jth one.
Arguments supporting
the plausibility of some of the assumptions (1-5), may be found
in the paper by Maeshiro and Kimura 1.
In our analysis, all possible mutations are considered for each
position at the codon. A change in a single nucleotide of the codon
leads to a codon change, but not necessarily to a change in the
coded amino acid. Thus the mutation 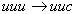 correspond
to a "change" from phenylalanine (Phe) to phenylalanine;
in other words, to a silent mutation. Otherwise, the mutation correspond
to a "change" from phenylalanine (Phe) to phenylalanine;
in other words, to a silent mutation. Otherwise, the mutation 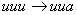 corresponds
to a change form phenylalanine (Phe) to leucine (Leu). corresponds
to a change form phenylalanine (Phe) to leucine (Leu).
Once all possible mutations for each position at the codon were
taken into account, via simple addition of corresponding amino acid
changes we obtain the transition matrix 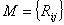 . .
Furthermore, for a given amino acid its concentration will change
according to:
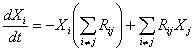 (1) (1)
At equilibrium,
the "concentrations" will reach constant values, thus
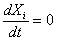 , and
the system is easily workable out on the following constraint: , and
the system is easily workable out on the following constraint:
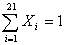 (2) (2)
Constructing a
new matrix from the elements of 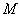 ,
and computing the corresponding determinants, it is possible to find
out ,
and computing the corresponding determinants, it is possible to find
out 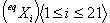 . .
Data and
programs
Data were downloaded from the codon usage database at www.zakusa.jp.
Special programs were developed by one of us (CMO) for estimating
the transition matrix M from the data, as well as for computing
equilibrium composition and the real amino acid composition of each
species.
Results
The initial
part of this section is devoted to the properties of the transition
matrix M and its relevance for the equilibrium concentrations. If
the case were that all elements of the matrix M are identical (
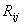 =1, for
all i, j), then at equilibrium the concentration of each amino acid
will be constant: =1, for
all i, j), then at equilibrium the concentration of each amino acid
will be constant: 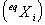 =
(1/21) =0.0476. =
(1/21) =0.0476.
Taking into account (1), it is easy to show that the farther the
system is from equilibrium the faster will be its evolution towards
it.
Some properties
of the transition matrix.
Some easy to interpret properties may be drawn from the matrix M
(Table I). As apparent, nearly 25% of all point mutations are silent
(corresponding to diagonal elements of M). Roughly 48% of all mutations
are silent or toward an amino acid from the same class (e. g. from
Valine to Alanine, of from Glutamate to Aspartate and vice versa).
The number of zeros in the matrix M (57% of the total) suggests
the presence of a large amount of amino acid changes that cannot
be achieved via a single mutation. This is reflected in the so-called
"Matrices of Mutation Costs for Amino acids".
Matrix M is symmetric, and it endows it with some properties as
it can be seen later.
In their studies, Freeland and Hurst 2 selected
a huge number of hypothetical codes, with codons corresponding to
different amino acids. Their codon assignment was not completely
random, since they divided the ''codon space'' (i.e., the 64 possible
codons) into the 21 non-overlapping sets of codons observed in the
natural code, each set comprising all codons specifying a particular
amino acid in the natural code (20 sets for the amino acids and
1 set for the 3 stop codons). They generated each alternative code
by randomly assigning each of the 20 amino acids to one of these
sets. Whereas all three stop codons remain invariant in position
for all alternative codes.
As result of their procedure each of the generated "genetic
codes" is topologically similar to the SGC. If one keeps the
same topology (even when the coded amino acids are different), this
warranties that always 25% of the mutations will be silent. In this
sense, no matter how huge the selected number of codes is, it corresponds
to a limited subset of all the possible codes.
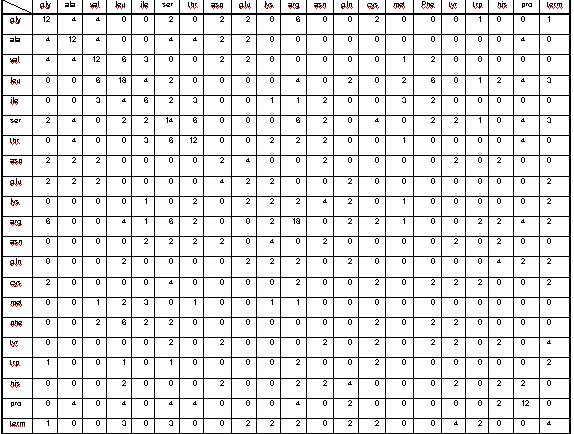
Table I Matrix M obtained from the proposed model with no codon
usage preference. Notice the abundance of large elements on the
diagonal, corresponding to silent mutations.
Equilibrium concentrations.
A plausible property expected from M's symmetry is that at equilibrium
all the 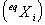 =
(1/21) =0.0476. At the same time, small departures from symmetry
lead to an uneven distribution of amino acid compositions at equilibrium. =
(1/21) =0.0476. At the same time, small departures from symmetry
lead to an uneven distribution of amino acid compositions at equilibrium.
Effect of
codon usage.
Matrix 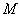 was obtained
on the assumption 1 being valid. For some amino acids this seems
to be the case, for example the codons corresponding to phenylalanine
in Homo sapiens (differing less than in 20%). However, the
synonymic representation is very uneven for some amino acids as
Leucine, where the codons UUA and CUG differ in their usage by more
than a factor of five. was obtained
on the assumption 1 being valid. For some amino acids this seems
to be the case, for example the codons corresponding to phenylalanine
in Homo sapiens (differing less than in 20%). However, the
synonymic representation is very uneven for some amino acids as
Leucine, where the codons UUA and CUG differ in their usage by more
than a factor of five.
Codon usage changes from species to species. Considering uneven
codon usage makes the matrix M asymmetric, and this is reflected
in the equilibrium concentrations..
We rearranged the matrix 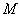 for the case of codon usage (codon usage tables were downloaded
from www.zakusa.jp) on the condition that the sum of frequencies
for a given amino acid equals to the number of corresponding synonyms.
We realize that this is not the only possible assumption, but it
may be illustrative for understanding the consequences of codon
usage manipulations. The corresponding equilibrium concentrations
are shown in Table II. As it can be noticed, considering the uneven
codon usage can lead to noticeable departures from the even distribution
corresponding to the case with identical codon usage. In the case
of the Human Immunodeficiency Virus, at equilibrium, the most abundant
amino acid (glutamate) exceeds the less abundant (triptophane) by
a factor of 1.77. At the same time, these results suggest that the
effect of codon usage in a realistic scenario never will lead to
departures greater than 35% respect to the theoretical value of
0.047. To elucidate whether or not codon usage differences
do play a convenient role for keeping one or another distribution
of amino acids remains an open question.
for the case of codon usage (codon usage tables were downloaded
from www.zakusa.jp) on the condition that the sum of frequencies
for a given amino acid equals to the number of corresponding synonyms.
We realize that this is not the only possible assumption, but it
may be illustrative for understanding the consequences of codon
usage manipulations. The corresponding equilibrium concentrations
are shown in Table II. As it can be noticed, considering the uneven
codon usage can lead to noticeable departures from the even distribution
corresponding to the case with identical codon usage. In the case
of the Human Immunodeficiency Virus, at equilibrium, the most abundant
amino acid (glutamate) exceeds the less abundant (triptophane) by
a factor of 1.77. At the same time, these results suggest that the
effect of codon usage in a realistic scenario never will lead to
departures greater than 35% respect to the theoretical value of
0.047. To elucidate whether or not codon usage differences
do play a convenient role for keeping one or another distribution
of amino acids remains an open question.
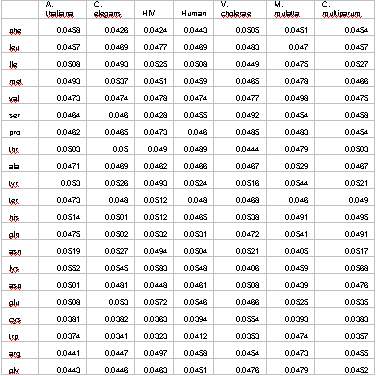
Table II. Equilibrium concentration for different species. Codon
usage frequencies were taken into account.
Behavior
of real data.
The amino acid compositions of many species are today available
at the web (e. g. at the "Zakusa" website). This allows
exploring the predictions of our model with real data from many
species. Here we approach the question of how far different species
are from equilibrium.
Figure 1 shows the result of our analysis for 3 different species.
As it can be seen, several amino acids are close to their theoretical
equilibrium values. This is the case of phenylalanine, Isoleucine,
aspartate, and glutamine in humans. However, some amino acids systematically
diverge from equilibrium, regardless the species. This is the case
of leucine, whose proportion is always higher than the equilibrium
value and the stop command (Term), which always is below. An explanation
for the case of the stop codon is that we are looking at functional
proteins occurring in real species. If a gene is functional, it
will have one or few stop codons. Otherwise it would lead to an
unviable protein. Besides, special reparation mechanisms must be
developed during evolution for preventing mutations leading to the
stop codon. It is not excluded that a similar mechanism is operating
for preventing any mutation leading to the substitution of Leucine
and other amino acids that retain a high biological importance for
the protein function. The need to explore the consequences of a
selective mutation repairing mechanism emerges as a task related
to our model.
On the other hand, for each species there is different degree of
divergence from equilibrium.
We computed the area of the difference between real values and theoretical
equilibrium for 15 different species.
This has been represented in fig 2. These results suggest that eukaryotes
and prokaryotes are separated by this criterion. A special place
corresponds to HIV, for which this distance s low compared to both
eukaryotes and prokaryotes.
LUCA and preserved sequences. The availability of large proteins
data bases allows comparing proteins with similar function that
are phylogenetically distant. This has allowed, via a top-down approach,
to predict the better conserved sequences in evolution as well as
the protein composition of the Last Universal Common Ancestor (LUCA)
5. If our model is valid, the preserved sequences
6 as well as LUCA must be farther from equilibrium
respect to the non-preserved sequences and the contemporary species
respectively. The data behaved in accordance with predictions, as
they are summarized in table III.
| Non-preserved
sequences |
0,368 |
| Preserved
sequences |
0,5325 |
| Modern |
0,4251 |
| LUCA |
0,5236 |
Table
III. Distances from equilibrium for contemporary and early sequences.
A closer look at the changes in amino acid composition with respect
to LUCA revealed that in all but five of the amino acids the changes
were in accordance with the equilibrium criteria derived from our
model 7. An interesting coincidence is that the
five non-corresponding amino acids according to different criteria
8 were not present in the prebiotic environment,
and may be regarded as late debutants into biological evolution
7.
Discussion.
Attempts to
make congruent the evolution theory with the fact that there are
mechanisms for (hopefully unchanged) inheritance have amazed more
than one mind 8. The present paper is not an
attempt to cope with some of the formidable tasks posed on that
field. However, a very candid view to the problem, with a simple
model of the SGC under the pressure of evenly distributed mutations
can outline some plausible scenarios describing where amino acid
composition of the coded proteins can evolve to. Thus, our model
shows how differences in codon usage can lead to different amino
acid compositions at the end stage of this "evolution".
According to this model real species differ in their distance
from equilibrium. The fact that the HIV, a species where no or
little reparation takes place during the replication process,
is closer than other species to equilibrium may find an explanation.
Perhaps this may provide some clues to unexplored aspects of the
HIV future as a species. Becoming closer to equilibrium the species
will loose its mutation potential and the variability will be
reduced, perhaps attenuating one of the most difficult to fight
aspect of the HIV.
In chemistry, the concept of equilibrium is clear: concentrations
remain constant whereas at molecular level transitions are taking
place all the time. It is not so simple to conceive what the concept
of "equilibrium" introduced here can mean. It may be
conceived as a stage where no further changes in amino acid composition
will take place, though mutations in individual proteins will
be there. However, the overall rate of amino acid changes will
be much lower. This does not mean that there will be no changes
in species' phenotypic properties. The example of sickle cell
anemia illustrates how substantial the changes induced by a single
point mutation can be.
The study of real data has allowed to describe how amino acids
are being changed in different proteins 10.
The "PAM" and "BLOSOM" Matrices may be regarded
as very useful tools summarizing how these mutations occur. From
our model it is possible to predict how a PAM matrix will look
like. The degree of similarity between prediction and reality
can tell us about the validity of this simple assumptions as well
as the possible weight of other factors not considered in it.
The origin of the genetic code has been a matter of discussion
already for almost 40 years 9, 11.
Arguments and results found so far can either support or disregard
any of the hypotheses available. Our model cannot clarify this
question, however, other questions, as that of the putative amino
acid composition millions of years ago can be treated in the framework
of our model. With knowledge about the real mutation rates it
is also possible to suggest the future evolution of the amino
acid composition for each species.
Thus, we find that the SGC is endowed not only with properties
that allow minimal changes under the effect of mutation load.
It also can provide useful information about important aspects
of evolution (as the case is of amino acid composition of proteins),
as well as the pace at which these changes are taking place under
conditions of unchanged mutation load. Other aspects, as a description
of the expected evolution of amino acid composition or its previous
behavior may be outlined in the framework of this approach. Our
predictions, compared with data obtained by other methods about
the composition of early biological forms are encouraging at this
stage.
Acknwledgements:
JLHC is a Senior Associate of the AS-ICTP and would like toacknowledge
the Centre for financial support. Authors thank professors Julian
Chela-Flores and Roberto Cruz-Rodes (From the AS-ICTP) for encouragement
and suggestions, and Ricardo Franklin (Nuclear Physics Faculty at
Havana) for useful discussions. This work was prepared during JLHC's
stay at the AS- ICTP in September 2004.
Bibliografía
1. Maeshiro, T and Kimura M. The role of robustness
and changeability on the origin and evolution of genetic codes.
Proc. Natl. Acad. Sci. U S A. 28; 95 (9): 5088-5093 (1998)
2.
Freeland, S. and Hurst, L. The genetic code is one in a million.
J. Mol. Evol. 47, 238:248 (1998).
3.
Ardell, D. On error-minimization in a sequential origin of the standard
genetic code. J. Mol.Evol. 47, 1:13 (1998).
4.
V.R. Chechetkin Block structure and stability of the genetic code
Journal of Theoretical Biology 222, 177-188 (2003).
5. Carl Woese The universal ancestor. Proc. Natl.
Acad. Sci. U S A. 95, 6854-6859 (1998).
6.
Arun K. A., Kuo-Bin L. and Praveen I. Rapid detection of conserved
regions in protein sequences using wavelets. In Silico Biology 4,
0013 (2004);
7.
D. J. Brooks and J. R. Fresco. Increased Frequency of Cysteine,
Tyrosine, and Phenylalanine Residues Since the Last Universal Ancestor.
Mol. Cell. Proteomics 1, 125 - 131 (2002).
8.
D. J. Brooks, J. R. Fresco, A. M. Lesk, and M. Singh. Evolution
of Amino Acid Frequencies in Proteins Over Deep Time: Inferred Order
of Introduction of Amino Acids into the Genetic Code. Mol. Biol.
Evol., 19, 1645 - 1655 (2002).
9.
Crick, F. The origin of the genetic code. J. Mol. Biol. 38,
367-379 (1968).
10.
Henikoff S, Henikoff JG.Amino acid substitution matrices from protein
blocks. Proc Natl. Acad. Sci. U S A.; 89:10915-10919 (1992).
11.
DiGiulio, M. Reflections on the origin of the genetic code: a hypothesis.
J.Theor. Biol. 191, 191:196 (1998).
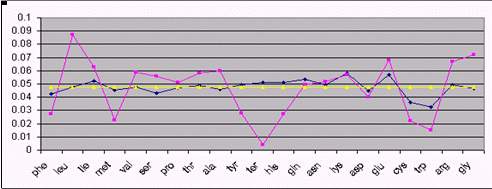
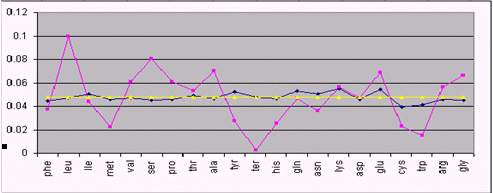
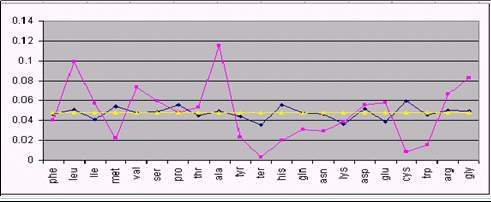
Fig 1. Comparison between real amino acid composition (cyan), and
equilibrium composition with (yellow) and without (dark blue) codon
usage correction. From top to bottom: HIV, Human and the bacterium
Agrobacter.
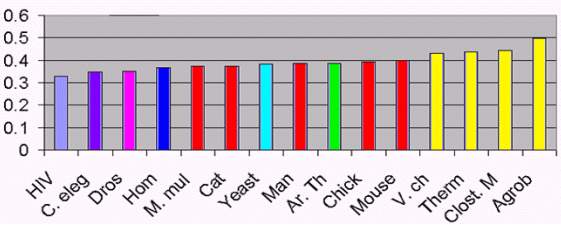
Figure 2. Distance from equilibrium for a group of species.
|




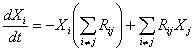 (1)
(1)




